

2달 만에 본계로 참가했다.
부계로 계속 못 올라가는 게 현타 와서 마음을 다 비우고 본계로 했는데 약간 올랐다...
한동안 1800 퍼포 이상을 찍어본적이 없었는데 아이디에 적응하는 건가....?
CF 1473A. Replacing Elements
배열의 어떤 원소를 다른 두 원소의 합으로 바꿀 수 있다.
이때, 배열의 모든 원소를 d 이하로 만들 수 있는지에 대한 문제이다.
기본적으로 주어지는 모든 원소가 d 이하이면 아무런 작업을 하지 않아도 된다.
만약 d보다 큰 원소가 하나 이상 존재한다면, 해당 원소를 바꿔주는 최적의 경우는
배열의 모든 원소 중 제일 작은 값 2개를 골라 바꿔주는 경우이므로, 배열을 오름차순으로 정렬하여 A[1] + A[2]가 d이하이면 YES이다.
[소스코드]
#include<bits/stdc++.h>
using namespace std;
int A[101];
int main(void) {
ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
int T; cin >> T;
while (T--) {
int n, d; cin >> n >> d;
int mx = 0;
for (int i = 1; i <= n; i++) cin >> A[i];
sort(A + 1, A + 1 + n);
if (A[n] <= d || A[1] + A[2] <= d) cout << "YES\n";
else cout << "NO\n";
}
}
CF 1473B. String LCM
약수, 배수 관계를 문자열에 적용하는 방식이다.
어떤 문자열 a가 b로 나누어 떨어진다는 것은 b가 a의 연속된 부분 문자열인 경우이다.
lcm(s, t)를 구하기 위해서는 lcm(|s|, |t|)을 구해서 s를 lcm(|s|, |t|) / |s| 만큼, t를 lcm(|s|, |t|) / |t| 만큼 각각 이어 붙였을 때 두 문자열이 동일한지 확인해주면 된다.
[소스 코드]
#include<bits/stdc++.h>
#define sz(x) (int)x.size()
using namespace std;
int main(void) {
ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
int T; cin >> T;
while (T--) {
string a, b; cin >> a >> b;
string s1, s2;
for (int i = 1; i <= lcm(sz(a), sz(b)) / sz(a); i++) s1 += a;
for (int i = 1; i <= lcm(sz(a), sz(b)) / sz(b); i++) s2 += b;
if (s1 == s2) cout << s1 << '\n';
else cout << -1 << '\n';
}
}
CF 1473C. No More Inversions
많은 사람들이 proof by AC로 푼 문제이다.
라운드 도중에는 무수히 많은 예제들을 만들어보며 어찌어찌 풀이를 구해 믿음의 제출을 했지만, 정확하게 논리적으로 이 문제를 푼다면 난이도가 훨씬 높을 것 같다.
문제는 n과 k가 주어지고, 1,2,3, ..., k-1, k, k-1, k-2, ..., k-(n-k) 로 총 n개의 원소로 이루어진 배열 a가 주어진다.
그리고 또 다른 수열 b를 permutation P로 만드는데, b[i] = p[a[i]] 로 구성된다.
최종적으로, 수열 b의 i < j && b[i] > b[j]인 inversion 쌍의 개수가 수열 a의 inversion 쌍의 개수보다 작거나 같으면서
사전 순으로 가장 크도록 만들어주는 permutation P를 구하는 문제이다.
자세한 풀이는 editorial을 참고하자..

[소스 코드]
#include<bits/stdc++.h>
using namespace std;
int main(void) {
ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
int T; cin >> T;
while (T--) {
int n, k; cin >> n >> k;
if (n == k) for (int i = 1; i <= n; i++) cout << i << ' ';
else {
for (int i = 1; i <= 2 * k - 1 - n; i++) cout << i << ' ';
for (int i = k; i > 2 * k - 1 - n; i--) cout << i << ' ';
}
cout << '\n';
}
}
CF 1473D. Program
문자열로 '+'와 '-'로 이루어진 연산의 순서가 주어진다.
x = 0부터 시작해서 순서대로 +이면 1을 더하고, -이면 1을 빼주는 연산을 진행하는데,
[l, r] 쿼리가 주어질 때, [l, r] 구간의 연산을 제외하고 순서대로 진행했을 때 만들어지는 x값의 가짓수를 구하는 문제이다.
개인적으로 C보다 더 쉽게 느껴졌고, 꽤 많은 사람들이 비슷하게 느낀 것 같다.
C는 코드는 매우 짧지만 정확한 증명이 매우 어렵다.
일단 만들어지는 x값의 가짓수는 연산과정에서의 x의 최솟값과 최댓값을 구하면 된다.
1 또는 -1이 더해지므로 최솟값과 최댓값 사이에 만들어질 수 없는 값은 존재하지 않는다.
[l, r] 쿼리가 주어지면, 먼저 l-1번째까지의 최솟값과 최댓값을 구한다.
그리고 [l, r] 쿼리를 고려하지 않았을 때의 r번째 값과 [r+1, n]에서의 최솟값과 최댓값을 각각 구한 후,
[r+1, n]에서 값이 얼마만큼 변하는지를 확인한다.
결국, prefix와 suffix들의 최소 최대 전처리를 해두면 각 쿼리마다 O(1)에 해결 가능하다.
라운드 도중에는 구간의 최소, 최대를 세그먼트 트리로 구현하여 쿼리마다 O(logn)에 계산하였다.
[소스 코드]
#include<bits/stdc++.h>
#define sz(x) (int)x.size()
using namespace std;
using pii = pair<int, int>;
const int MAX = (int)2e9;
int A[200001];
pii range[200001];
int mi_tr[800001];
int mx_tr[800001];
int init(int x, int s, int e, bool mi) {
if (s == e) {
if (mi) return mi_tr[x] = A[s];
else return mx_tr[x] = A[s];
}
if (mi) return mi_tr[x] = min(init(x * 2, s, (s + e) / 2, mi), init(x * 2 + 1, (s + e) / 2 + 1, e, mi));
else return mx_tr[x] = max(init(x * 2, s, (s + e) / 2, mi), init(x * 2 + 1, (s + e) / 2 + 1, e, mi));
}
int query(int x, int s, int e, int l, int r, bool mi) {
if (s > r || e < l) {
if (mi) return MAX;
else return -MAX;
}
if (s >= l && e <= r) {
if (mi) return mi_tr[x];
else return mx_tr[x];
}
if (mi) return min(query(x * 2, s, (s + e) / 2, l, r, mi), query(x * 2 + 1, (s + e) / 2 + 1, e, l, r, mi));
else return max(query(x * 2, s, (s + e) / 2, l, r, mi), query(x * 2 + 1, (s + e) / 2 + 1, e, l, r, mi));
}
int main(void) {
ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
int T; cin >> T;
while (T--) {
int n, m; cin >> n >> m;
for (int i = 1; i <= n; i++) {
range[i].first = 0;
range[i].second = 0;
}
for (int i = 1; i <= 4 * n; i++) {
mi_tr[i] = 0;
mx_tr[i] = 0;
}
string s; cin >> s;
for (int i = 0; i < sz(s); i++) {
if (s[i] == '+') A[i + 1] = 1;
else A[i + 1] = -1;
}
for (int i = 1; i <= n; i++) {
A[i] += A[i - 1];
range[i].first = min(range[i - 1].first, A[i]);
range[i].second = max(range[i - 1].second, A[i]);
}
init(1, 1, n, false); init(1, 1, n, true);
for (int i = 1; i <= m; i++) {
int l, r; cin >> l >> r;
if (r == n) {
cout << range[l - 1].second - range[l - 1].first + 1 << '\n';
continue;
}
int mi = query(1, 1, n, r + 1, n, true);
int mx = query(1, 1, n, r + 1, n, false);
int now = A[l - 1];
int R = now + mx - A[r];
int L = now - (A[r] - mi);
cout << max(R, range[l - 1].second) - min(L, range[l - 1].first) + 1 << '\n';
}
}
}
CF 1473E. Minimum Path
라운드가 끝나고 나서 이 문제의 풀이를 들었을 때, 뒤통수를 한 대 맞은 기분이었다.
이걸 이렇게 생각할 수 있구나 하고 감탄했다... 경험의 차이인 걸까
문제는 단순하다. 무방향 연결 그래프가 주어져있고, 간선마다 가중치가 존재한다.
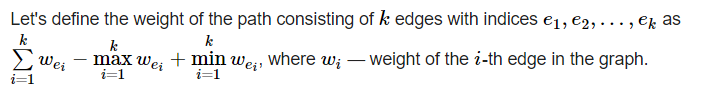
1번 노드로부터 각 노드로 갈 때, 이 값이 최소가 되는 경로를 찾아주는 것이다.
즉, 위의 수식을 경로의 길이라고 한다면, 1번 노드를 제외한 나머지 노드별로 최단거리를 구해주면 된다.
핵심적인 아이디어는, 경로를 구한 뒤에 간선들 중 최댓값과 최솟값을 뽑아주는 것이 아니라,
2번 더해질 간선과 0번 더해질 간선을 하나씩 고르는 방식이다.
결국 최대인 간선은 더해지지 않는 셈이고, 최소인 간선은 두 번 더해지는 셈이니 각 간선 별로 2번 더해지거나 0번 더해지는 모든 경우들을 다 고려한다면 최단거리가 구해지게 된다.
따라서 dijkstra 배열을 dis[N][2][2]로 선언하여, 지금까지 2번 더해진 간선과 0번 더해진 간선이 각각 존재하는지를 판단한다.
[소스 코드]
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
using pll = pair<ll, ll>;
vector<pll>adj[200001];
ll dis[200001][2][2];
int main(void) {
ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
int n, m; cin >> n >> m;
for (int i = 1; i <= m; i++) {
ll u, v, w; cin >> u >> v >> w;
adj[u].push_back({ v, w });
adj[v].push_back({ u, w });
}
for (int i = 1; i <= n; i++) {
dis[i][0][0] = dis[i][0][1] = dis[i][1][0] = dis[i][1][1] = 1e18;
}
dis[1][0][0] = 0;
priority_queue<tuple<ll, ll, int, int >> pq;
pq.push(make_tuple(0LL, 1LL, 0, 0));
while (!pq.empty()) {
auto[cost, u, a, b] = pq.top();
pq.pop();
cost = -cost;
if (cost > dis[u][a][b]) continue;
for (auto[v, w] : adj[u]) {
ll new_dis = cost + w;
if (dis[v][a][b] > new_dis) {
dis[v][a][b] = new_dis;
pq.push(make_tuple(-dis[v][a][b], v, a, b));
}
if (a == 0 && b == 0 && dis[v][1][1] > new_dis) {
dis[v][1][1] = new_dis;
pq.push(make_tuple(-dis[v][1][1], v, 1, 1));
}
if (a == 0 && dis[v][1][b] > new_dis + w) {
dis[v][1][b] = new_dis + w;
pq.push(make_tuple(-dis[v][1][b], v, 1, b));
}
if (b == 0 && dis[v][a][1] > new_dis - w) {
dis[v][a][1] = new_dis - w;
pq.push(make_tuple(-dis[v][a][1], v, a, 1));
}
}
}
for (int i = 2; i <= n; i++) cout << dis[i][1][1] << ' ';
}
PC로 보시는 것을 권장합니다.
피드백은 언제나 환영입니다. 댓글로 달아주세요 ^-^
'프로그래밍 대회 풀이 > Codeforces' 카테고리의 다른 글
| [Codeforces] Round #705 (Div. 2) A ~ D 풀이 (0) | 2021.03.08 |
|---|---|
| [Codeforces] Round #559 (Div. 2) A ~ E 풀이 (0) | 2021.03.07 |
| [Codeforces] Round #552 (Div. 3) A ~ E 풀이 (0) | 2021.01.11 |
| [Codeforces] Round #694 (Div. 2) 풀이 (0) | 2021.01.07 |
| [Codeforces] Round #551 (Div. 2) A ~ D 풀이 (2) | 2021.01.04 |



