Rank = 861 (KR 37)

1. K-Goodness String (12 pts)
길이가 N인 문자열 S가 주어지고, 각 글자를 원하는 만큼 변경할 수 있다.
1≤i≤N/2 인 i에 대해서 S[i] != S[N-i+1]인 i의 개수가 K가 되기 위한 최소 변경 횟수를 구하는 문제이다.
단순 구현 문제이다. S[i]나 S[N-i+1] 둘 중 하나를 바꾼다면 상태를 바꿀 수 있으니 처음 문자열에서 S[i] != S[N-i+1]인 i의 개수를 구한 다음 K와의 차이만큼 문자를 바꿔주면 된다.
(멍청하게도 S[i] == S[N-i+1]이면 점수를 얻는다고 생각해서 1WA를 받았다. 왜 하필 예제 답이 같아서...)
[소스 코드]
#include<bits/stdc++.h>
using namespace std;
int main(void) {
ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
int T; cin >> T;
for (int t = 1; t <= T; t++) {
int n, k; cin >> n >> k;
string s; cin >> s;
int cnt = 0;
for (int i = 1; i <= n / 2; i++) {
if (s[i - 1] != s[n - i]) cnt++;
}
cout << "Case #" << t << ": " << abs(cnt - k) << '\n';
}
}
2. L Shaped Plots (20 pts)
0 또는 1로 채워진 R x C 격자판이 주어진다. 격자판 내에 다음 조건을 만족하는 L 모양의 개수를 구하는 문제이다.
조건 1) 1로 채워진 격자로만 구성되어야 한다.
조건 2) L 모양에서 긴 변의 길이가 짧은 변의 길이의 정확히 2배이어야 한다. (각 변의 길이는 교점을 포함한다)
조건 3) 짧은 변의 길이는 최소 2이다.
조건을 만족하는 예시는 다음과 같다.

조건을 만족하지 않는 경우는 다음과 같다.
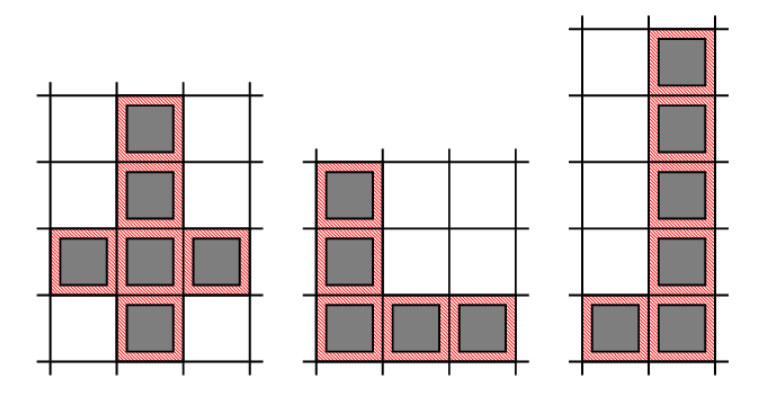
기본적으로 L 모양을 만들기 위해서는 (2, 4), (3, 6), (4, 8),.... 들의 쌍이 가능하다.
R과 C의 범위가 최대 1000이므로 대략적으로 O(R*C) 정도에 해결해야 함을 알 수 있다. 대충 칸을 한 번씩만 탐색해서 구할 수 있어야 한다는 의미이다.
따라서, L 모양을 특정한 칸부터 시작해서 만들 때 가장 쉽게 만드는 방법으로, 현재 칸을 A[i][j]라고 했을 때 A[i][j]가 L 모양에서의 꼭짓점일 때를 고려한다.
(꼭짓점이 아니라면 언제 꺾여야 하는지를 모두 고려해야 하며 시간이 오래 걸린다)
그러면 꼭짓점에서 상하좌우 방향으로 뻗어나가는 방식으로 생각할 수 있는데, L 모양을 만들기 위해서는 상/하 중에서 하나, 좌/우 중에서 하나를 고르는 총 4가지 경우를 고려하면 된다.
이제 L 모양의 개수는 어떻게 구할까?
A[i][j]에서 상/하/좌/우로 각각 뻗어나갈 수 있는 최대의 범위를 구한다. 즉, A[i][j]부터 연속된 1의 최대 개수를 구한다.
예를 들어 A[i][j]부터 위로 연속된 1이 최대 6개 있고, 오른쪽으로 연속된 1이 최대 4개 있다고 가정하자.
가능한 쌍을 (위, 오른쪽)로 나타낼 때, (4, 2), (6, 3), (2, 4)가 가능하다.
이를 일반화하면 위로 u만큼, 오른쪽으로 r만큼 뻗어나갈 수 있다고 가정할 때,
u가 L 모양의 긴 변인 경우는 min(u/2, r) - 1만큼 만들 수 있고, r이 긴 변인 경우에는 min(r/2, u) - 1만큼 만들 수 있다.
(조건 3에 의해서 -1)
이런 방식으로 4가지 경우를 모두 구해주면 된다. 상하좌우로 뻗어나갈 수 있는 범위는 미리 전처리를 해두면 최종적으로 O(RC)만에 해결할 수 있다.
[소스 코드]
#include<bits/stdc++.h>
using namespace std;
int a[1010][1010];
int D[1010][1010];
int U[1010][1010];
int L[1010][1010];
int R[1010][1010];
int main(void) {
ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
int T; cin >> T;
for (int t = 1; t <= T; t++) {
int r, c; cin >> r >> c;
for (int i = 1; i <= r; i++) {
for (int j = 1; j <= c; j++) {
cin >> a[i][j];
D[i][j] = U[i][j] = L[i][j] = R[i][j] = a[i][j];
}
}
for (int j = 1; j <= c; j++) {
for (int i = r - 1; i >= 1; i--) {
if (a[i][j] == 1) D[i][j] += D[i + 1][j];
}
for (int i = 2; i <= r; i++) {
if (a[i][j] == 1) U[i][j] += U[i - 1][j];
}
}
for (int i = 1; i <= r; i++) {
for (int j = 2; j <= c; j++) {
if (a[i][j] == 1) L[i][j] += L[i][j - 1];
}
for (int j = c - 1; j >= 1; j--) {
if (a[i][j] == 1) R[i][j] += R[i][j + 1];
}
}
int ans = 0;
for (int i = 1; i <= r; i++) {
for (int j = 1; j <= c; j++) {
ans += max(min(L[i][j] / 2, U[i][j]) - 1, 0);
ans += max(min(U[i][j] / 2, L[i][j]) - 1, 0);
ans += max(min(L[i][j] / 2, D[i][j]) - 1, 0);
ans += max(min(D[i][j] / 2, L[i][j]) - 1, 0);
ans += max(min(R[i][j] / 2, U[i][j]) - 1, 0);
ans += max(min(U[i][j] / 2, R[i][j]) - 1, 0);
ans += max(min(R[i][j] / 2, D[i][j]) - 1, 0);
ans += max(min(D[i][j] / 2, R[i][j]) - 1, 0);
}
}
cout << "Case #" << t << ": " << ans << '\n';
}
}
3. Rabbit House (24 pts)
각 칸에 0 이상의 정수가 부여된 R x C 격자판이 주어진다. 각 칸마다 숫자를 증가시킬 수만 있을 때, 모든 칸이 인접한 칸과의 차이가 1 이하가 되도록 만드는 최소 증가 횟수를 구하는 문제이다.
일단 이미 값이 제일 큰 칸은 증가시키지 않고 그대로 두는 게 최적임을 쉽게 알 수 있다.
그리고, 인접한 칸에 의해서 반드시 증가되어야 하는 만큼만 증가시켜도 충분하다.
따라서 가장 높은 칸들부터 먼저 보면서 인접한 칸들을 키워나가는 방식으로 해결할 수 있고 이는 다익스트라로 해결할 수 있다.
다만, 각 칸별 반드시 증가시켜야 하는 높이를 구해주어야 하므로 기존에 최소 거리를 구하는 것과는 반대로 최댓값을 구해주어야 한다.
[소스 코드]
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int, int>;
int a[301][301];
int tmp[301][301];
int dx[4] = { 0, 1, 0, -1 };
int dy[4] = { 1, 0, -1, 0 };
int main(void) {
ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
int T; cin >> T;
for (int t = 1; t <= T; t++) {
int r, c; cin >> r >> c;
ll ans = 0;
priority_queue<pair<int, pii>> pq;
for (int i = 1; i <= r; i++) {
for (int j = 1; j <= c; j++) {
cin >> a[i][j];
tmp[i][j] = a[i][j];
pq.push({ a[i][j], {i, j} });
}
}
while (!pq.empty()) {
int cost = pq.top().first;
auto [x, y] = pq.top().second;
pq.pop();
if (cost < tmp[x][y]) continue;
tmp[x][y] = cost;
for (int i = 0; i < 4; i++) {
int nx = x + dx[i];
int ny = y + dy[i];
if (nx >= 1 && nx <= r && ny >= 1 && ny <= c) {
if (tmp[nx][ny] < cost - 1) {
tmp[nx][ny] = cost - 1;
pq.push({ cost - 1, {nx, ny} });
}
}
}
}
for (int i = 1; i <= r; i++) {
for (int j = 1; j <= c; j++) {
ans += tmp[i][j] - a[i][j];
}
}
cout << "Case #" << t << ": " << ans << '\n';
}
}
4. Checksum (44 pts)
0 또는 1로 이루어진 N x N 행렬 A가 존재한다. 그리고 A의 각 행별 원소들을 xor 한 값을 저장한 배열인 R, 각 열별 원소들을 xor한 값을 저장한 배열인 C를 만든다.
그 후에, A의 일부 원소들을 잊어버렸고, 이를 R과 C를 이용해서 복원을 할 수 있으면 복원을 하던지, 혹은 각 원소별로 측정되어있는 비용을 지불해서 복원을 해야 할 때, 모든 원소를 복원하기 위한 최소 비용을 구하는 문제이다.
아이디어를 떠올리기가 많이 어려운 문제이다. 다른 사람의 풀이를 참고했다.
행렬의 원소가 0 또는 1인 경우는 빈칸으로 나타내겠다. 간단한 2x2 격자판을 생각해보자.

이런 경우가 주어지면 항상 R과 C를 이용해서 -1로 주어진 원소를 복원할 수 있다.
화살표 방향에 해당하는 행 또는 열로 구해낼 수 있게 된다.
하지만 네 칸이 모두 -1인 경우에는 R과 C를 이용해서 찾을 수 없으므로 최소 하나의 칸에 대해서는 비용을 지불해야 한다.
이를 참고해서 생각해보면 A[i][j]가 복원가능한 경우는 A[i][j]를 제외하고 i행을 모두 알고 있거나, 혹은 j열을 모두 알고있는 경우이다.
그럼 반대로 생각해서, A[i][j]가 복원 불가능한 경우는 위와 같은 경우가 존재하지 않아야 하므로 -1이 포함된 모든 행과 열들은 최소 2개 이상의 -1을 포함하고 있어야 한다는 의미이다.
이를 그림으로 나타내 보면 사이클의 형태를 띠고 있음을 알 수 있다.

따라서 행렬 A가 복원될 수 있기 위해서는 복원되지 않은 칸들을 연결했을 때 사이클이 없어야 한다는 점에서 최소 스패닝 트리(MST)를 떠올릴 수 있다.
최소 비용을 지불해서 일부 칸을 복원하여 사이클이 없도록 만들어주는 것은, 전체 비용에서 최대 비용을 가지는 스패닝 트리를 빼주는 것과 동일하다. 나머지 칸들을 비용을 지불하여 복원시켜주면 된다.
각 행과 열을 하나의 정점으로 생각하고, (i, j)를 i행과 j열을 연결하는 간선이라고 생각해서 비용이 큰 순서대로 스패닝 트리를 만들어가면 된다.
지금까지의 풀이만 보면 R배열과 C배열은 전혀 생각하지 않았다. 그 이유는 다음과 같다.
R배열과 C배열로 주어진 xor값만 만족하도록 A를 복원하면 되는데, 두 칸만 이용하면 다른 칸과 관계없이 원하는 xor값을 만들 수 있음을 알 수 있다.
따라서 만약 A[i][j] = -1이고, i행과 j열에 포함된 -1의 개수가 각각 3개 이상이라면 A[i][j]를 0 또는 1로 임의로 부여를 해도 무방하다. 나머지 원소들로 xor값을 조절할 수 있기 때문이다.
결국 위의 그림과 같이 각 행과 열에 반드시 -1이 2개씩만 오는 경우를 생각해볼 수 있는데, 이 또한 임의로 부여해도 상관없다. 그 이유는, xor값은 두 개의 칸만으로도 모든 경우를 다 만들 수 있기 때문이다. xor값이 0인 경우는 (0, 0) 또는 (1, 1), 1인 경우는 (0, 1) 또는 (1, 0)이면 된다.
즉, 위와 같은 사이클의 형태가 나온다면 특정 칸을 복원할 때에는 0으로 복원하던지 1로 복원하던지 둘 다 원래의 A를 만들 수 있는 것이다.
따라서 사실 R과 C 배열은 문제풀이에 전혀 영향을 미치지 않기 때문에 무시해도 된다. 복원된 배열을 구할 필요 또한 없기 때문이다.
[소스 코드]
#include<bits/stdc++.h>
#define ini(x, y) memset(x, y, sizeof(x));
using namespace std;
using pii = pair<int, int>;
int a[501][501], b[501][501], r[501], c[501], P[1010];
int find(int a) {
return P[a] < 0 ? a : P[a] = find(P[a]);
}
void merge(int a, int b) {
a = find(a);
b = find(b);
if (a != b) {
if (P[a] > P[b]) swap(a, b);
P[a] += P[b];
P[b] = a;
}
}
int main(void) {
ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
int T; cin >> T;
for (int t = 1; t <= T; t++) {
int n; cin >> n;
ini(P, -1);
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
cin >> a[i][j];
}
}
int total = 0;
int mx = 0;
priority_queue<pair<int, pii>> pq;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
cin >> b[i][j];
total += b[i][j];
pq.push({ b[i][j], {i, n + j} });
}
}
for (int i = 1; i <= n; i++) cin >> r[i];
for (int i = 1; i <= n; i++) cin >> c[i];
while (!pq.empty()) {
int cost = pq.top().first;
auto[x, y] = pq.top().second;
pq.pop();
if (find(x) != find(y)) {
mx += cost;
merge(x, y);
}
}
cout << "Case #"<<t<<": "<<total - mx << '\n';
}
}