[문제]
https://www.acmicpc.net/problem/1396
1396번: 크루스칼의 공
첫째 줄에는 그래프의 정점의 개수 n과 간선의 개수 m이 주어진다. 그리고 두 번째 줄에서 m+1번째 줄까지는 a b c의 형태로 a와 b를 잇는 간선의 고유값이 c라는 의미이다. m+2번째 줄에는 알고 싶은
www.acmicpc.net
[난이도]
- Platinum I (21.06.10 기준)
[필요 개념]
- Union-Find
- Parallel Binary Search (병렬 이분 탐색) or LCA
[풀이]
이 문제는 크게 두 풀이로 나뉜다. 첫 번째로는 PBS(병렬 이분 탐색)이다. 흔히 PBS의 대표 예제 문제로 알려져 있는데, 조만간 PBS에 대한 글을 따로 작성할 예정이라 자세한 풀이는 생략할 것이다.
두 번째로는 LCA를 이용한 풀이인데, 되게 아이디어가 참신하다고 생각해서 포스팅을 해보려고 한다. (이미 고수들 사이에선 웰논이라는 얘기가...)
1. PBS (병렬 이분 탐색)
이 문제의 쿼리가 1개라고 가정해보자.
그렇다면 간선을 정렬한 다음 크루스칼 알고리즘을 이용하여 가중치가 작은 간선부터 연결해가다가 x와 y가 연결되는 순간의 가중치와 범위에 있는 정점의 개수를 구해주면 된다.
따라서 시간복잡도는 간선을 정렬하는 O(mlogm)과 union 하는데 필요한 O(m*α(n)), 사실상 O(m)의 합이다.
그러므로 쿼리가 Q개 있다면 간선을 정렬해둔다음, Q번 크루스칼 알고리즘을 사용해야 하므로
O(mlogm + Qm)이 되어 시간안에 수행하지 못한다.
이를 해결하기 위해서 PBS를 이용하는데, 오프라인으로 쿼리를 모두 저장해둔 다음 각 쿼리마다 이분 탐색을 동시에 진행하는 것이다.
자세한 방법은 (링크)를 확인하자.
[소스 코드]
#include<bits/stdc++.h>
#define all(v) v.begin(), v.end()
#define ini(x, y) memset(x, y, sizeof(x));
#define pb push_back
#define fi first
#define se second
using namespace std;
using pii = pair<int, int>;
int P[101010], l[101010], r[101010];
pii ans[101010];
vector<int> g[101010];
int find(int a) {
return P[a] < 0 ? a : P[a] = find(P[a]);
}
void merge(int a, int b) {
a = find(a);
b = find(b);
if (a != b) {
if (P[a] > P[b]) swap(a, b);
P[a] += P[b];
P[b] = a;
}
}
int main(void) {
ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
int n, m; cin >> n >> m;
vector<tuple<int, int, int>> edge;
for (int i = 0; i < m; i++) {
int a, b, c; cin >> a >> b >> c;
edge.pb(make_tuple(c, a, b));
}
sort(all(edge));
int q; cin >> q;
vector<pii> query(q);
for (int i = 0; i < q; i++) {
cin >> query[i].fi >> query[i].se;
}
for (int i = 0; i < q; i++) l[i] = 1, r[i] = m;
while (1) {
for (int i = 1; i <= m; i++) g[i].clear();
bool chk = false;
for (int i = 0; i < q; i++) {
if (l[i] <= r[i]) {
chk = true;
g[(l[i] + r[i]) / 2].pb(i);
}
}
if (!chk) break;
ini(P, -1);
int i = 1;
for (auto [c, a, b] : edge) {
merge(a, b);
for (int j : g[i]) {
if (find(query[j].fi) == find(query[j].se)) {
ans[j].fi = c;
ans[j].se = abs(P[find(query[j].fi)]);
r[j] = i - 1;
}
else l[j] = i + 1;
}
i++;
}
}
for (int i = 0; i < q; i++) {
if (l[i] > m) cout << -1 << '\n';
else cout << ans[i].fi << ' ' << ans[i].se << '\n';
}
}
2. LCA
LCA를 이용하면 온라인으로 각 쿼리에 대한 답을 계산할 수 있다.
우선, 간선을 가중치의 오름차순으로 정렬하는 것은 동일하다.
그 다음 차례대로 (x, y) 간선을 연결해가는데, x와 y가 아직 연결되지 않았다면 새로운 정점을 만들어 x가 속한 컴포넌트와 y가 속한 컴포넌트를 자식으로 갖도록 연결한다.
말로 이해하기 어려우니 아래의 그림을 참고해보자. (문제의 예제를 이용하였다)
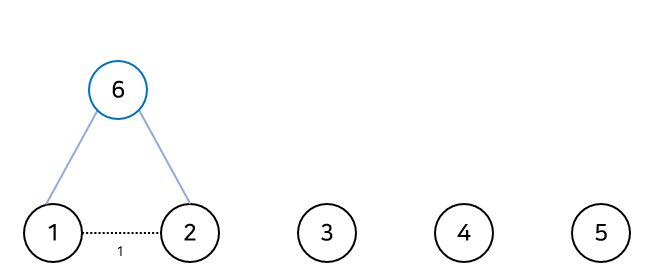
가중치가 제일 작은 간선인 (1, 2)를 연결해줄 때, 1과 2를 연결해주는 것이 아니라 1과 2를 자식으로 갖는 새로운 정점을 만들어준다.

그다음은 2와 3을 연결하는데, 마찬가지로 2와 3을 연결하는 것이 아니라 2가 포함된 컴포넌트와 3이 포함된 컴포넌트를 자식으로 갖는 새로운 정점을 만들어준다. 즉, 각 컴포넌트의 루트를 자식으로 연결해준다.
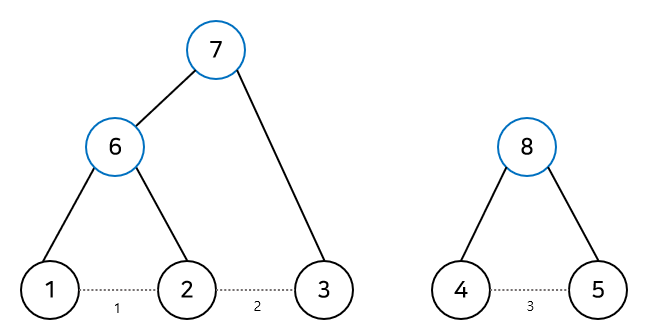
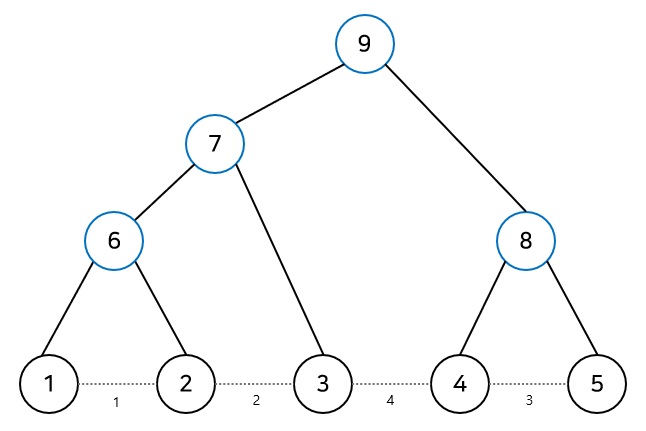
이제 이렇게 만들어준 트리를 어떻게 이용할까?
잘 생각해보면, 어느 두 정점 x와 y가 처음으로 서로 연결이 되는 시점은 두 정점의 공통 선조가 생기는 시점이다.
그리고, 간선의 가중치가 작은 순서대로 연결을 해왔기 때문에 x에서 y로 갈 수 있는 최소 온도는 x와 y의 최소 공통 조상인 정점, 즉 LCA인 정점이 생성되는 시점의 간선의 가중치이다.
따라서 트리를 구성할 때 새로운 정점이 만들어지면 현재 간선의 가중치를 해당 정점에 저장해둔다.

이러면 x에서 y로 가기 위한 최소 온도(L)는 lca(x, y)로 쉽게 구할 수 있다.
그때 공이 움직일 수 있는 범위에 포함되는 정점의 개수는 어떻게 될까?
L보다 큰 가중치의 간선들은 아직 반영되지 않았기 때문에 lca(x, y) 위로는 연결된 정점이 없다.
그리고 lca(x, y) 아래로는 모두 L보다 작은 가중치의 간선들로 연결되었기 때문에 결국 lca(x, y)를 루트로 하는 서브 트리의 크기가 답이 된다.
[소스 코드]
#include<bits/stdc++.h>
#define all(v) v.begin(), v.end()
#define pb push_back
using namespace std;
int n, m, q;
vector<int> adj[202020];
int par[202020][19], lv[202020], P[202020], w[202020], s[202020];
int find(int a) {
return P[a] < 0 ? a : P[a] = find(P[a]);
}
void dfs(int u, int p, int level) {
lv[u] = level;
for (int v : adj[u]) {
if (v == u) continue;
par[v][0] = u;
dfs(v, u, level + 1);
}
}
int lca(int x, int y) {
if (lv[x] > lv[y]) swap(x, y);
for (int i = 18; i >= 0; i--) {
if (lv[y] - lv[x] >= (1 << i)) {
y = par[y][i];
}
}
if (x == y) return x;
for (int i = 18; i >= 0; i--) {
if (par[x][i] != par[y][i]) {
x = par[x][i];
y = par[y][i];
}
}
return par[x][0];
}
int main(void) {
ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
cin >> n >> m;
vector<tuple<int, int, int>> edge;
for (int i = 0; i < m; i++) {
int a, b, c; cin >> a >> b >> c;
edge.pb(make_tuple(c, a, b));
}
sort(all(edge));
memset(P, -1, sizeof(P));
for (int i = 1; i <= n; i++) s[i] = 1;
for (auto [c, a, b] : edge) {
a = find(a); b = find(b);
if (a != b) {
adj[++n].pb(a);
adj[n].pb(b);
P[a] = n;
P[b] = n;
w[n] = c;
s[n] = s[a] + s[b];
}
}
for (int i = 1; i <= n; i++) {
if (P[i] < 0) dfs(i, i, 0);
}
for (int j = 1; j <=18; j++) {
for (int i = 1; i <= n; i++) {
par[i][j] = par[par[i][j - 1]][j - 1];
}
}
cin >> q;
while (q--) {
int x, y; cin >> x >> y;
if (find(x) != find(y)) cout << -1 << '\n';
else {
int L = lca(x, y);
cout << w[L] << ' ' << s[L] << '\n';
}
}
}
P.S. 다른 문제에서 떠올리기는 쉽지 않겠지만 유용하게 쓰일 수 있을 것 같은 트릭이다.... 어떻게 이런 발상을 할 수 있을까?
'알고리즘 > 백준 문제풀이' 카테고리의 다른 글
| Platinum DP 문제들 풀이 (1) (2) | 2021.05.24 |
|---|---|
| [BOJ 20190] 버블버블 (3) | 2020.12.28 |
| [BOJ 17353] 하늘에서 떨어지는 1, 2, ..., R-L+1개의 별 (2) | 2020.12.22 |
| [BOJ 7812] 중앙 트리 (2) | 2020.12.14 |
| [BOJ 9202] Boggle (0) | 2020.12.13 |
