Atcoder Beginner Contest 205 (ABC 205) 풀이

오랜만에 참가한 ABC인데, 마침 오랜만에 ABC 문제들이 괜찮아서 풀이를 작성해보려고 한다. 결과도 나쁘지 않았다.

문제 링크 : https://atcoder.jp/contests/abc205/tasks

공식 해설 : https://atcoder.jp/contests/abc205/editorial

(*) = 난이도

A. Kcal (*6)

단순 계산 문제이다. 100ml당 A kcal을 얻을 수 있을 때 Bml이 있으면 몇 kcal를 얻을 수 있는지를 구하면 된다.

#include<bits/stdc++.h>
using namespace std;
int main(void) {
	ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
	double a, b; cin >> a >> b;
	cout << fixed;
	cout.precision(10);
	cout << a * (b / 100);
}

B. Permutation check (*16)

N개의 원소로 이루어진 수열이 주어질 때, 이 수열이 Permutation인지를 판단해야 한다.

오름차순으로 정렬하고, 모든 i에 대해 A[i] = i인지만 체크하면 된다.

#include<bits/stdc++.h>
using namespace std;

int a[1010];
int main(void) {
	ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
	int n; cin >> n;
	for (int i = 1; i <= n; i++) cin >> a[i];
	sort(a + 1, a + 1 + n);
	for (int i = 1; i <= n; i++) {
		if (a[i] != i) {
			return cout << "No", 0;
		}
	}
	cout << "Yes";
}

C. POW (*63)

$A, B, C$ 가 주어질 때, $A^C$ 와 $B^C$ 를 대소 비교하는 문제이다. A와 B가 음수인지 양수인지에 따라 케이스 분류를 해주면 된다.

#include<bits/stdc++.h>

using namespace std;
int main(void) {
	ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
	int a, b, c; cin >> a >> b >> c;
	if (c % 2 == 0 || (a >= 0 && b >= 0)) {
		if (abs(a) > abs(b)) cout << '>';
		else if (abs(a) < abs(b)) cout << '<';
		else cout << '=';
	}
	else {
		if (a < 0 && b >= 0) cout << '<';
		else if (a >= 0 && b < 0) cout << '>';
		else {
			if (abs(a) > abs(b)) cout << '<';
			else if (abs(a) < abs(b))cout << '>';
			else cout << '=';
		}
	}

}

D. Kth Excluded (*713)

N개의 원소로 이루어진 수열 A가 주어지고, Q개의 쿼리가 주어지는데, 각 쿼리마다 A에 포함된 원소를 제외한 양의 정수 중에서 K번째로 작은 수를 구하는 문제이다. K번째로 작은 수를 ans라고 하자.

수열 A의 원소와 K의 범위가 $10^{18}$ 이므로, 나이브하게 구할 수는 없다.

먼저 K이하인 A의 원소가 존재하지 않는다면 ans = K이다. 하지만 만약 K이하인 A의 원소가 r개 있다면 적어도 ans >= K + r이다.

이때, K+1 ~ K+r 범위인 A의 원소가 또 존재한다면 그만큼 다시 ans를 증가시켜줘야 하며, 이 과정을 ans가 증가하지 않을 때까지 반복해주어야 한다.

이를 이분탐색으로 계속 확인하면서 이전보다 포함되는 A의 원소의 개수가 증가했는지를 판단하여 증가하지 않으면 현재 값이 답이 된다.

#include<bits/stdc++.h>
using namespace std;
using ll = long long;

ll a[101010];
int main(void) {
	ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
	int n, q; cin >> n >> q;
	for (int i = 1; i <= n; i++) cin >> a[i];
	for (int i = 1; i <= q; i++) {
		ll k; cin >> k;
		int prv = 0;
		while (1) {
			int cnt = upper_bound(a + 1, a + 1 + n, k) - a - 1;
			if (cnt != prv) {
				k += cnt - prv;
				prv = cnt;
			}
			else {
				cout << k << '\n';
				break;
			}
		}
	}
}

E. White and Black Balls (*2025)

N개의 흰 공과 M개의 검은 공을 일렬로 배치하는 경우의 수 중, 1부터 N+M까지의 모든 i에 대해서 [1, i]에 있는 흰 공의 개수 w와 검은 공의 개수 b에 대해서 w ≤ b + K를 만족하는 경우의 수를 구하는 문제이다.

디스크립션은 간단하다.

대회 중에 해결하지 못한 문제이다. 해설을 보고 나서야 웰논인 문제임을 깨달았다. K가 0이라면 올바른 괄호 문자열의 개수를 구할 때 사용하는 카탈란 수와 관련된 문제와 매우 유사하다.

언뜻 보면 dp스럽지만 N과 M이 100만이라 dp가 잘 떠오르지 않았다. 아마 안되지 않을까 싶다...

이 문제를 2차원 좌표평면상으로 가져와보자. 흰 공을 y축, 검은 공을 x축이라고 생각하면, N개의 흰 공과 M개의 검은 공을 일렬로 배열하는 경우의 수는 가로/세로로 1칸씩 이동할 수 있다고 할 때, (0, 0)에서 (M, N)으로 가는 경우의 수와 동일하다.

가로/세로로 1칸 이동하는 것을 검은/흰 공을 1개 이어 붙이는 것과 동일하게 생각할 수 있다.

그러면 조건을 만족하지 않는 경우는 언제일까?

위의 그림에서 (0, 0)에서 (M, N)으로 이동하는 과정에서 한번이라도 y = x + K 직선 위로 올라가는 경우는 조건을 만족하지 않는 경우이다. y > x + K 즉, w > b + K인 경우이기 때문이다.

이는 반드시 y = x + K+1를 한번 이상은 만난다는 의미가 된다.

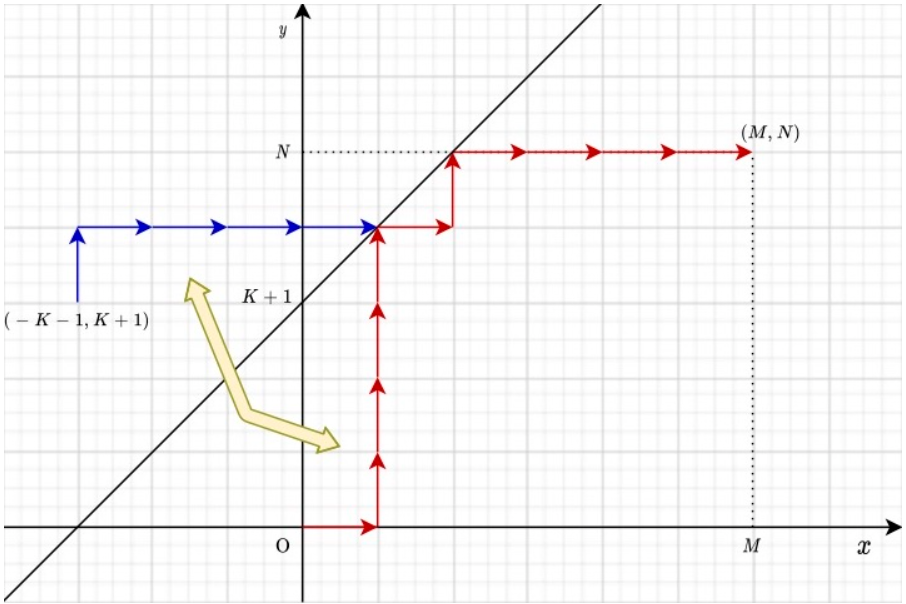
위 그림과 같이 (0, 0)을 y = x + K+1에 대해 점대칭을 시킨 (-K-1, K+1)를 생각해보자. (-K-1, K+1)에서 (M, N)으로 가는 경로는 반드시 y = x + K+1와 만나게 되며, 그 교점을 P라고 하면 (0, 0) ~ P의 경우의 수와 (-K-1, K+1) ~ P의 경우의 수가 동일하다.

따라서, 조건을 만족하지 않는 경우의 수는 (-K-1, K+1)에서 (M, N)으로 가는 경우의 수와 동일하다.

N > M + K인 경우에는 항상 0인 점을 주의하자.

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int MOD = (int)1e9 + 7;

#define MN 2000000
ll fac[MN + 10], facinv[MN + 10];
ll mpow(ll a, ll x) {
	ll res = 1;
	while (x > 0) {
		if (x % 2) res = (res*a) % MOD;
		a = (a*a) % MOD;
		x /= 2;
	}
	return res;
}
void fac_init() {
	fac[0] = 1;
	for (int i = 1; i <= MN; i++) fac[i] = fac[i - 1] * i % MOD;
	facinv[MN] = mpow(fac[MN], MOD - 2);
	for (int i = MN - 1; i >= 0; i--) facinv[i] = facinv[i + 1] * (i + 1) % MOD;
}
ll C(ll n, ll r) {
	return ((fac[n] * facinv[r]) % MOD) * facinv[n - r] % MOD;
}
int main(void) {
	ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
	fac_init();
	int n, m, k; cin >> n >> m >> k;
	if (n > m + k) cout << 0;
	else cout << (MOD + C(n + m, n) - C(n + m, m + k + 1)) % MOD;
}

F. Grid and Tokens (*2088)

H x W 격자판이 있고, N개의 블록을 격자판에 놓으려고 한다. (H, W, N≤100)

2가지 조건이 있는데, 각 블럭은 각자 주어진 A, B, C, D 값에 따라 (A, C)를 왼쪽 위, (B, D)를 오른쪽 아래 꼭짓점으로 하는 직사각형의 범위에만 놓을 수 있으며 같은 행과 열에는 2개 이상의 블록을 놓을 수 없다.

이때, 놓을 수 있는 블럭의 최대 개수를 구하는 문제이다.

이 문제는 최대유량 알고리즘으로 해결할 수 있다. 먼저 A, B, C, D 조건이 없이, 같은 행과 열에 2개 이상 놓을 수 없다는 조건만으로 그래프 모델링을 해보자.

같은 행에 2개 이상 놓을 수 없으므로, 소스(S)에서 각 행별로 용량이 1인 간선을 연결해주면 같은 행에 2개 이상 들어가지 않는다.

그다음, 각 행에서 모든 열로 용량이 1인 간선을 연결해주고, 각 열 별로 싱크(T)로 용량이 1인 간선을 연결해주면, 같은 열에 2개 이상 들어갈 수 없으면서 행과 열을 연결하면 블록이 들어갈 위치가 정해지게 된다.

즉, 다음과 같은 형태로 이루어진다.

그런데 여기에 조건이 하나 추가된다.

각 블럭별로 놓을 수 있는 범위가 주어지기 때문에, 각 블록별로 가능한 행과 열이 제한된다.

따라서, 블럭도 함께 그래프 모델링을 해줘야 한다.

행과 열 사이에 블럭을 넣고, 각 블록별로 가능한 행과 열에 모두 연결을 해주면 행과 열이 매칭 되는 것이 블록을 (행, 열)에 놓는 것과 동일하다.

다만, 블럭은 한 번만 사용될 수 있으므로 정점 분할을 통해서 블록이 여러 번 사용되는 것을 방지해준다.

#include<bits/stdc++.h>
using namespace std;
const int MAX = (int)2e9;

#define MAX_V 510
int S, T;
struct Dinic {
	struct edge {
		int v, c, rev;
		edge(int v, int c, int rev) : v(v), c(c), rev(rev) {}
	};
	int n;
	vector<vector<edge>> adj;
	vector<int> level, see;
	Dinic(int n) : n(n) {
		adj.assign(n + 1, vector<edge>());
		level.assign(n + 1, -1);
		see.assign(n + 1, 0);
	}
	void addedge(int u, int v, int capa) {
		adj[u].push_back({ v, capa, (int)adj[v].size() });
		adj[v].push_back({ u, 0, (int)adj[u].size() - 1 });
	}
	bool bfs() {
		level.assign(n + 1, -1);
		queue<int> q;
		level[S] = 0;
		q.push(S);
		while (!q.empty()) {
			int u = q.front(); q.pop();
			for (auto i : adj[u]) {
				if (level[i.v] == -1 && i.c > 0) {
					level[i.v] = level[u] + 1;
					q.push(i.v);
				}
			}
		}
		return level[T] != -1;
	}
	int dfs(int u, int flow) {
		if (u == T) return flow;
		for (; see[u] < (int)adj[u].size(); see[u]++) {
			auto i = adj[u][see[u]];
			if (level[i.v] == level[u] + 1 && i.c > 0) {
				int now = dfs(i.v, min(flow, i.c));
				if (now > 0) {
					adj[u][see[u]].c -= now;
					adj[i.v][adj[u][see[u]].rev].c += now;
					return now;
				}
			}
		}
		return 0;
	}
	int solve() {
		int ret = 0;
		while (bfs()) {
			see.assign(n + 1, 0);
			while (1) {
				int flow = dfs(S, MAX);
				if (!flow) break;
				ret += flow;
			}
		}
		return ret;
	}
};
int main(void) {
	ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
	int h, w, n; cin >> h >> w >> n;
	S = 0;
	T = 501;
	Dinic dc = Dinic(MAX_V);
	//S = 0, 행 : 1 ~ 100, piece = 101~200, 201~300, 열 : 301~400, T = 501
	for (int i = 1; i <= h; i++) dc.addedge(S, i, 1);
	for (int i = 1; i <= w; i++) dc.addedge(300+i, T, 1);
	for (int i = 1; i <= n; i++) {
		dc.addedge(100 + i, 200 + i, 1);
		int a, b, c, d; cin >> a >> b >> c >> d;
		for (int j = a; j <= c; j++) {
			dc.addedge(j, 100 + i, 1);
		}
		for (int j = b; j <= d; j++) {
			dc.addedge(200 + i, 300 + j, 1);
		}
	}
	cout << dc.solve();
}

저작자표시 비영리 동일조건

'프로그래밍 대회 풀이 > Atcoder' 카테고리의 다른 글

Atcoder Beginner Contest 206 (ABC 206) 풀이 (3)	2021.06.20
Atcoder Beginner Contest 185 (ABC 185) 풀이 (0)	2020.12.13

내 블로그 - 관리자 홈 전환	`Q` `Q`
새 글 쓰기	`W` `W`

글 수정 (권한 있는 경우)	`E` `E`
댓글 영역으로 이동	`C` `C`

이 페이지의 URL 복사	`S` `S`
맨 위로 이동	`T` `T`
티스토리 홈 이동	`H` `H`
단축키 안내	`Shift` + `/` `⇧` + `/`

Rebro의 코딩 일기장

Atcoder Beginner Contest 205 (ABC 205) 풀이

'프로그래밍 대회 풀이 > Atcoder' 카테고리의 다른 글

티스토리툴바

단축키

내 블로그

블로그 게시글

모든 영역

Atcoder Beginner Contest 205 (ABC 205) 풀이

'프로그래밍 대회 풀이 > Atcoder' 카테고리의 다른 글

'프로그래밍 대회 풀이/Atcoder' Related Articles

티스토리툴바

단축키

내 블로그

블로그 게시글

모든 영역