2021 카카오 인턴십 for Tech developers 코딩 테스트 해설
2021년 카카오의 여름 인턴십의 첫 번째 관문인 코딩 테스트가 지난 2021년 5월 8일에 4시간에 걸쳐 진행되었습니다. 이번 인턴 코딩 테스트에서는 5문제가 출제되었습니다. 이전과 동일하게 쉬운
tech.kakao.com
2021 카카오 채용연계형 인턴십 코딩 테스트에 참가했다.
5문제를 해결하는데 2시간 조금 넘게 걸렸는데, 마지막 문제에만 1시간 넘게 소모했다... 대회를 준비한 사람이 아니라면 거의 풀기 힘든 문제가 아닐까 싶다.

생각보다 높은 난이도에 조금 당황했고, 프로그래머스에 적응이 잘 되지 않아서 약간의 어려움을 겪기도 했다. 일부러 코딩 테스트에 적응하고자 visual studio를 사용하지 않았는데, IDE를 사용하지 못하는 환경이나 hidden testcase가 존재하는 경우에서 실수를 더 줄일 필요가 있을 것 같다.
비록 아직 복무가 끝나지 않아 이후의 프로세스는 진행하지 못했지만, 겨울 인턴십은 끝까지 완주할 수 있었으면 좋겠다.
(본 글에 작성한 솔루션 코드들은 모두 실제 코딩 테스트 때 제출했던 코드이다.)
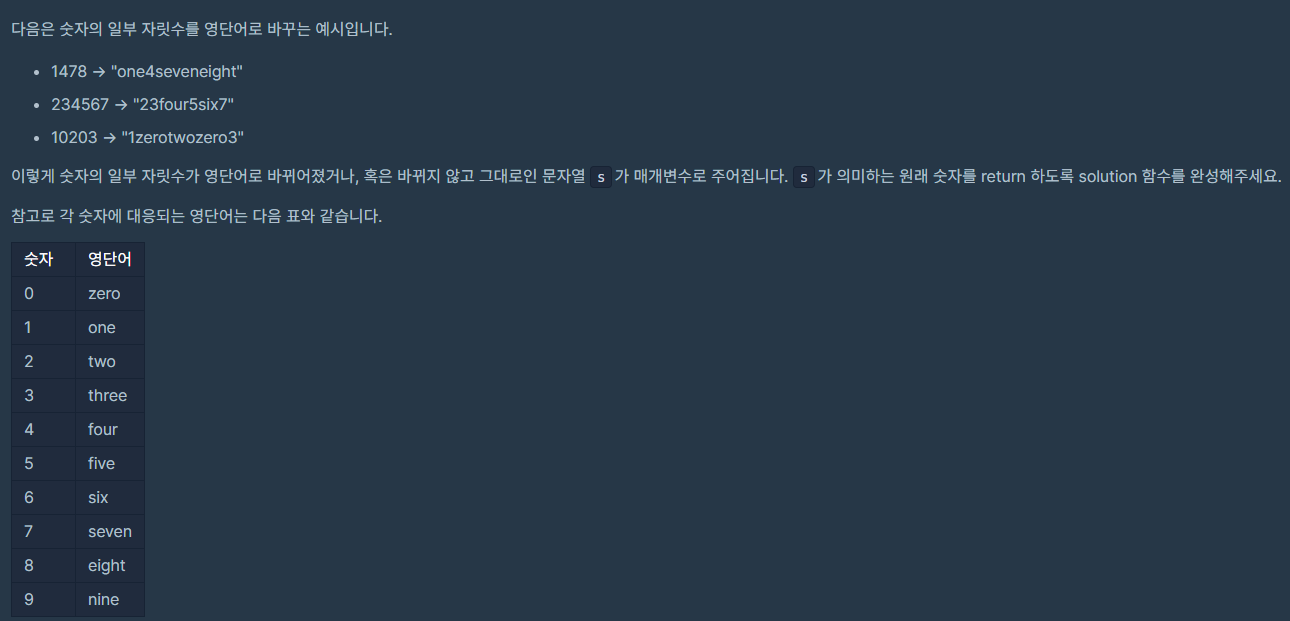
1. 숫자 문자열과 영단어
[알고리즘]
- 구현, 문자열 파싱(parsing)
[풀이]
숫자를 기준으로 문자열을 나눈 다음, 미리 map에 저장해둔 [단어 : 숫자] 쌍을 이용하여 숫자로 바꾸어준다.
#include <string>
#include <vector>
#include <map>
using namespace std;
int solution(string s) {
int answer = 0;
map<string, int> mp;
mp["zero"] = 0; mp["one"] = 1; mp["two"] = 2; mp["three"] = 3; mp["four"] = 4;
mp["five"] = 5; mp["six"] = 6; mp["seven"] = 7; mp["eight"] = 8; mp["nine"] = 9;
string tmp = "";
for (int i = 0; i < s.size(); i++) {
if (s[i] >= '0' && s[i] <= '9') answer = answer * 10 + s[i] - '0';
else {
tmp += s[i];
if (mp.find(tmp) != mp.end()) {
answer = answer * 10 + mp[tmp];
tmp.clear();
}
}
}
return answer;
}
* 거의 매번 나오는 문자열 파싱 문제이다. C++이 문자열 파싱에 있어서는 성능이 좋진 않지만, STL string이나 map을 잘 활용한다면, 큰 무리 없이 해결할 수 있을 것이다.
2. 거리두기 확인하기

[알고리즘]
- 그래프 탐색 (DFS)
[풀이]
대기실의 크기가 5x5로 매우 작다. 따라서 BFS가 아닌 DFS를 이용해도 시간에 큰 영향은 없다.
대기실의 각 칸을 한번 훑으면서, 응시자가 있는 경우에는 해당 위치로부터 거리가 2 이내에 다른 응시자가 존재하는지를 DFS로 탐색해준다.
#include <string>
#include <vector>
using namespace std;
int dx[4] = { 0, 1, 0, -1 };
int dy[4] = { 1, 0, -1, 0 };
bool chk;
void find(vector<string>& v, int x, int y, int X, int Y, int cnt) {
if (cnt == 2) return;
for (int i = 0; i < 4; i++) {
int nx = x + dx[i];
int ny = y + dy[i];
if (nx >= 0 && nx < 5 && ny >= 0 && ny < 5 && v[nx][ny] != 'X') {
if (nx == X && ny == Y) continue;
if (v[nx][ny] == 'P') {
chk = false;
return;
}
find(v, nx, ny, X, Y, cnt + 1);
}
}
}
vector<int> solution(vector<vector<string>> places) {
vector<int> answer;
for (auto v : places) {
bool flag = true;
for (int i = 0; i < 5; i++) {
for (int j = 0; j < 5; j++) {
if (v[i][j] == 'P') {
chk = true;
find(v, i, j, i, j, 0);
if (!chk) flag = false;
}
}
}
if (flag) answer.push_back(1);
else answer.push_back(0);
}
return answer;
}
* BFS/DFS 유형으로 매우 잘 알려져 있는 문제이다. DFS 코드가 조금 더 편리하긴 하지만, 주어지는 입력의 크기에 따라서 DFS를 선택하는 경우에 시간 초과가 발생할 수 있기 때문에 항상 문제 조건에 주의할 필요가 있다.
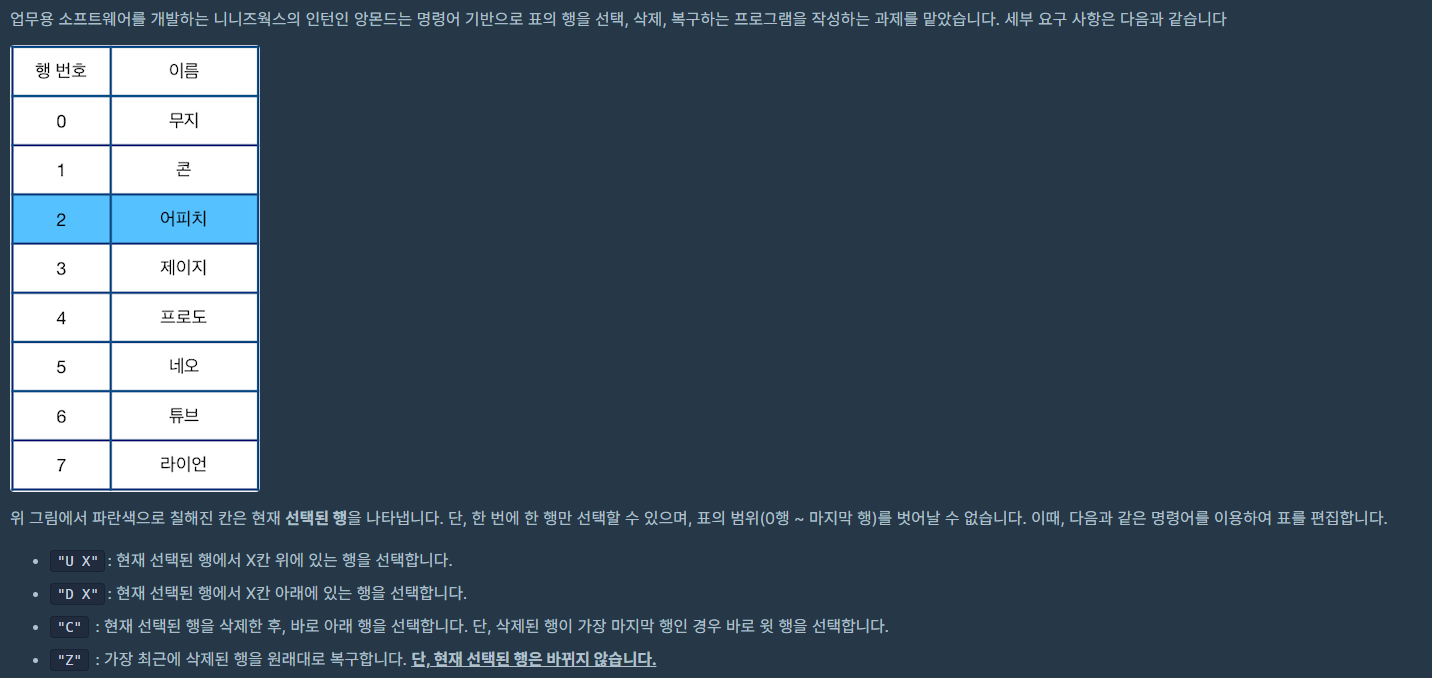
3. 표 편집
[알고리즘]
- set
[풀이]
문제에 대한 자세한 설명은 예시가 잘 나와있으므로 링크를 통해서 직접 읽어보는 것을 권장한다.
문제에서 수행해야 하는 연산은 다음과 같다.
1) 현재 원소보다 X칸 앞/뒤에 있는 원소로 이동한다.
2) 현재 원소를 삭제하고 그 뒤 원소로 이동한다. 만약 현재 원소가 제일 뒤라면 바로 앞의 원소로 이동한다.

3) 가장 마지막에 삭제된 원소를 다시 복구시킨다. (이동하진 않는다)
우선, 문제에서 주어지는 X값의 총합이 100만 이하라는 조건이 중요하다.
이는, 앞뒤로 이동하는 횟수가 최대 100만밖에 되지 않기 때문에, 로그(log) 시간에 이동해도 충분히 가능하다.
그리고 특정 원소를 삭제했을 때 이웃한 두 원소를 붙여주는 작업도 필요하다. 이는 STL set을 이용하면 상수 시간(반복자 이용) 내에 알아서 수행해주기 때문에 결국 set을 이용하면 이 문제를 간단하게 해결할 수 있다.
(배열을 이용하여 직접 원소들을 한 칸씩 밀어주는 방식을 사용하면 O(N)의 시간이 걸리게 되므로 효율성을 통과하지 못한다)
제일 먼저, set에 0부터 n-1까지의 정수를 다 넣어준다.
그다음, set.find 함수를 통해서 처음 위치의 반복자를 구해준다.
'U'또는 'D'이면 반복자를 앞, 뒤로 직접 이동시켜준다.
'C'이면 현재 원소를 삭제하는 경우인데, 현재 원소가 마지막 원소라면 앞의 원소로 이동하고, 그렇지 않으면 뒤의 원소로 이동한 후 이전에 가리키던 원소를 삭제한다.
그리고 삭제한 원소들은 스택에 저장하여 복구할 때 최근에 삭제한 원소부터 복구할 수 있도록 해준다.
'Z'는 원소를 복구하는 경우인데, 단순히 set에 추가만 해주면 자동으로 오름차순으로 정렬되고, 반복자가 가리키는 원소도 변함없다.
#include <string>
#include <vector>
#include <set>
#include <stack>
using namespace std;
string solution(int n, int k, vector<string> cmd) {
string answer = "";
set<int> s;
stack<int> erased;
for (int i = 0; i < n; i++) s.insert(i);
auto pos = s.find(k);
for (auto q : cmd) {
int x = 0;
if (q[0] == 'U') {
for (int i = 2; i < q.size(); i++) {
x = x * 10 + q[i] - '0';
}
while (x--) {
pos--;
}
}
else if (q[0] == 'D') {
for (int i = 2; i < q.size(); i++) {
x = x * 10 + q[i] - '0';
}
while (x--) {
pos++;
}
}
else if (q[0] == 'C') {
erased.push(*pos);
if (*pos == *s.rbegin()) {
pos--;
}
else pos++;
s.erase(erased.top());
}
else {
s.insert(erased.top());
erased.pop();
}
}
vector<int> chk(n);
for (auto i : s) {
chk[i] = 1;
}
for (int i = 0; i < n; i++) {
if (chk[i] == 1) answer += 'O';
else answer += 'X';
}
return answer;
}
* 이 문제에 대해서 세그먼트 트리나 펜윅 트리를 사용한 고수들이 꽤 많았는데, 카카오에서 제공한 공식 해설에도 이 풀이를 소개했다.
필자는 코딩 테스트에는 세그 트리를 이용할 수는 있지만 정해로는 절대 나오지 않는다는 생각으로 문제를 풀어서 애초에 이용할 생각조차 하지 않았는데, 공식 해설에도 등장한 만큼 앞으로는 이 정도 수준의 알고리즘까지 나올 수 있다는 마음가짐을 가져야 할 것 같다. (물론 카카오가 많이 어려운 편이긴 하다)
4. 미로 탈출


[알고리즘]
- 다익스트라 / 비트마스킹
[풀이]
문제를 요약하면, 단순히 최단거리를 구하는 문제에서 '함정'이라는 조건이 추가된 문제이다.
최대 10개의 함정이 존재하는데, 함정을 방문하게 되면 해당 함정과 연결된 모든 간선의 방향이 반대로 바뀌게 된다.
총 방의 개수(n)가 최대 1000개이고, 함정의 개수가 최대 10개이기 때문에, 각 방마다 전체 함정의 상태를 보관해도 대략 1000x1024의 dp table이면 충분하다.
함정의 상태는 각 함정마다 0 ~ 9의 번호를 붙인 다음 비트(bit)로 표현하여 비트가 켜져 있으면 해당 함정을 방문하여 간선이 뒤집어진 상태, 꺼져있으면 원래 간선인 상태로 나타낸다.
코드를 살펴보면, 먼저 서로 다른 두 방 사이에 직접 연결된 길이 여러 개 존재할 수 있고, 최단거리를 구하는 것이 목표이므로 가장 거리가 짧은 길만 남겨둔다.
그리고 방 사이를 이동할 때, 현재 방과 이동하는 방이 각각 함정인지 아닌지를 판단하고, 함정이라면 방문했는지를 판단하여 현재 간선의 방향을 확인한다.
#include <string>
#include <vector>
#include <queue>
#include <map>
#include <tuple>
const int MAX = (int)2e9;
using namespace std;
vector<int> adj[1010];
int dis[1010][1 << 11];
int solution(int n, int start, int end, vector<vector<int>> roads, vector<int> traps) {
int answer = MAX;
map<int, int> tnum;
map<pair<int, int>, int> edge;
map<pair<int, int>, int> revedge;
for (int i = 1; i <= n; i++) tnum[i] = 0;
for (int i = 0; i < traps.size(); i++) {
tnum[traps[i]] = i + 1;
}
for (int i = 0; i <= n; i++) {
for (int j = 0; j < (1 << 11); j++) dis[i][j] = MAX;
}
dis[start][0] = 0;
for (auto e : roads) {
if (edge.find({ e[0], e[1] }) == edge.end()) edge[{e[0], e[1]}] = e[2];
else edge[{e[0], e[1]}] = min(edge[{e[0], e[1]}], e[2]);
if (revedge.find({ e[1], e[0] }) == revedge.end()) revedge[{e[1], e[0]}] = e[2];
else revedge[{e[1], e[0]}] = min(revedge[{e[1], e[0]}], e[2]);
adj[e[0]].push_back(e[1]);
adj[e[1]].push_back(e[0]);
}
priority_queue<tuple<int, int, int>> pq;
pq.push(make_tuple(0, 0, start));
while (!pq.empty()) {
auto [cost, bit, u] = pq.top(); pq.pop();
cost = -cost;
for (int v : adj[u]) {
bool f1 = (bit & (1 << tnum[u]));
bool f2 = (bit & (1 << tnum[v]));
if ((f1 && f2) || (!f1 && !f2)) {
if (edge.find({ u, v }) != edge.end() && dis[v][bit] > cost + edge[{u, v}]) {
dis[v][bit] = cost + edge[{u, v}];
pq.push(make_tuple(-dis[v][bit], tnum[v] > 0 ? bit ^ (1 << tnum[v]) : bit, v));
}
}
else if ((f1 && !f2) || (!f1 && f2)) {
if (revedge.find({ u, v }) != revedge.end() && dis[v][bit] > cost + revedge[{u, v}]) {
dis[v][bit] = cost + revedge[{u, v}];
pq.push(make_tuple(-dis[v][bit], tnum[v] > 0 ? bit ^ (1 << tnum[v]) : bit, v));
}
}
}
}
for (int i = 0; i < (1 << 11); i++) {
answer = min(answer, dis[end][i]);
}
return answer;
}
5. 시험장 나누기


[알고리즘]
- 그리디, 파라메트릭 서치(Parametric Search), DFS
[풀이]
문제의 제한을 잘 살펴보자.
시험장의 수인 n이 최대 10000, 나눌 그룹의 수인 k는 n이하, 각 시험장의 응시자 수도 최대 10000명이다.
따라서 모든 간선 중에서 k개를 고르는 경우는 대략 $_{10000}C_k$ 이므로 당연히 효율성을 통과하지 못하게 된다.
n과 k가 매우 크기 때문에 그룹을 어떤 식으로 나눠야 가장 큰 그룹의 인원이 최소가 될지 감이 잘 잡히지 않는다.
그렇다면 어떻게 해결할 수 있을까?
이 문제는 파라메트릭 서치를 이용하여 관점을 조금 바꾸는 것이 중요하다.
문제에서는 "k개의 그룹으로 나누었을 때, 가장 큰 그룹의 최소 인원이 얼마인지" (최적화 문제)를 구하라고 하였는데,
이를 "가장 큰 그룹의 인원이 L 이하가 되도록 k개의 그룹으로 나눌 수 있는가?" (결정 문제)로 바꿔 생각할 수 있다.
이러면 위 문장을 만족하는 L값 중 가장 작은 값을 구하면 된다.
이렇게 최적화 문제를 결정 문제로 바꾸는 기법이 '파라메트릭 서치'이다.
여기서 최소의 L값은 이분 탐색으로 구할 수 있다.
그러면 이제 L값을 고정하면 어떤 식으로 그룹을 나누는 게 최적이 될까?
주어진 트리가 이진트리이기 때문에, 현재 노드가 최대 두 자식 중 한 자식의 그룹에 포함될 수 있는지를 판단한다.
만약 포함될 수 있다면 무조건 포함시키는 것이 이득이 된다.

예를 들어 6번 노드를 보면, L이 30이라고 가정할 때 3번 노드의 그룹에 포함될 수 있다. 따라서 하나의 그룹으로 묶어준다.
만약 가능한데도 불구하고 포함시키지 않았을 때 더 이득이 될 수 있을까? 그렇지 않다.
쉽게 이해할 수 있는데, 포함시키지 않는다면 당연히 3번 노드의 그룹에 남은 자리는 낭비되고, 다른 그룹에 6번 노드가 포함됨으로 인해 해당 그룹의 자리를 차지하게 되기 때문이다.
따라서 현재 노드에서 적용할 수 있는 후보들은 다음과 같다.
1) 자식들이 각각 속한 그룹과 현재 노드를 하나의 그룹으로 모두 묶을 수 있는 경우
2) 한 자식의 그룹에만 포함될 수 있는 경우
3) 어디에도 포함될 수 없는 경우
1)의 경우에는 자식 노드와 연결된 간선을 끊을 필요가 없다.
2)의 경우에는 연결되지 않은 자식은 더 이상 위에서 고려되지 않기 때문에, 그룹의 가중치 합이 더 적은 그룹에 속한 자식과 연결시켜준다.
3)의 경우에는 자식들과 연결된 간선을 모두 끊어줘야 한다.
이제 이 경우들을 한 번의 DFS로 리프 노드부터 타고 올라오면서 계산해줄 수 있다.
함수 반환 값으로 현재 노드가 속한 그룹의 가중치의 총합을 반환한다.
#include <iostream>
#include <string>
#include <vector>
const int MAX = (int)2e9;
using namespace std;
vector<int> adj[10101];
bool ch[10101];
int root;
int cnt;
bool can;
int dfs(int u, int m, vector<int>& num) {
if (num[u] > m) can = false;
int k1, k2;
if (adj[u].size() == 2) {
k1 = dfs(adj[u][0], m, num);
k2 = dfs(adj[u][1], m, num);
if (k1 + k2 + num[u] <= m) return k1 + k2 + num[u];
else {
if (k1 + num[u] > m && k2 + num[u] > m) {
cnt += 2;
return num[u];
}
else if (k1 + num[u] > m) {
cnt++;
return k2 + num[u];
}
else if (k2 + num[u] > m) {
cnt++;
return k1 + num[u];
}
else {
if (k1 > k2) {
cnt++;
return k2 + num[u];
}
else {
cnt++;
return k1 + num[u];
}
}
}
}
else if (adj[u].size() == 1) {
k1 = dfs(adj[u][0], m, num);
if (k1 + num[u] > m) {
cnt++;
return num[u];
}
else return k1 + num[u];
}
else {
return num[u];
}
}
bool sol(int k, int m, vector<int>& num) {
cnt = 0;
can = true;
dfs(root, m, num);
if (cnt >= k || !can) return false;
return true;
}
int solution(int k, vector<int> num, vector<vector<int>> links) {
int answer = MAX;
for (int i = 0; i < links.size(); i++) {
if (links[i][0] != -1) {
adj[i].push_back(links[i][0]);
ch[links[i][0]] = true;
}
if (links[i][1] != -1) {
adj[i].push_back(links[i][1]);
ch[links[i][1]] = true;
}
}
for (int i = 0; i < num.size(); i++) {
if (!ch[i]) root = i;
}
int s = 1;
int e = 1e8;
while (s <= e) {
int mid = (s + e) / 2;
if (sol(k, mid, num)) {
answer = min(answer, mid);
e = mid - 1;
}
else s = mid + 1;
}
return answer;
}
PC로 보시는 것을 권장합니다.
피드백은 언제나 환영입니다. 댓글로 달아주세요 ^-^
'기타 > 후기' 카테고리의 다른 글
| SUAPC 2021 Summer 참가 후기 (12) | 2021.08.29 |
|---|---|
| 2021 신촌 연합 알고리즘 여름 캠프 강사 후기 & PS 휴식기 (16) | 2021.08.19 |
| SUAPC 2021 Winter 대회 후기 (8) | 2021.03.02 |
| 2021 ICPC Sinchon Winter Algorithm Camp Contest 참가 후기 (3) | 2021.02.21 |
| 코드포스 블루, 퍼플 달성 후기 및 일지 & 공부법 (39) | 2020.11.13 |



