1725번 (히스토그램)

위의 문제는 분할 정복 알고리즘을 이용해서 해결할 수 있다.
분할 정복은 주어진 문제를 부분 문제들로 나누어 푸는 것이기 때문에 이 문제 또한 히스토그램을 나누어 푸는 것이 핵심이다.
따라서 주어진 n개의 막대그래프를 절반으로 나누게 되면 결국 찾고자 하는 가장 큰 직사각형은
다음 세가지중 하나에 속하게 된다.
1. 왼쪽 부분 문제에서 가장 큰 직사각형이 존재하는 경우
2. 오른쪽 부분 문제에서 가장 큰 직사각형이 존재하는 경우
3. 가장 큰 직사각형이 왼쪽 부분 문제와 오른쪽 부분 문제에 걸쳐 있는 경우
1번과 2번의 경우에는 재귀 호출을 이용하면 되고, 3번의 경우만 특별히 고려한다면 답을 구할 수 있을 것이다.

문제에서 출력이 20억을 넘지 않는다고 하였으니, 변수 자료형을 모두 int로 해도 무방하다.
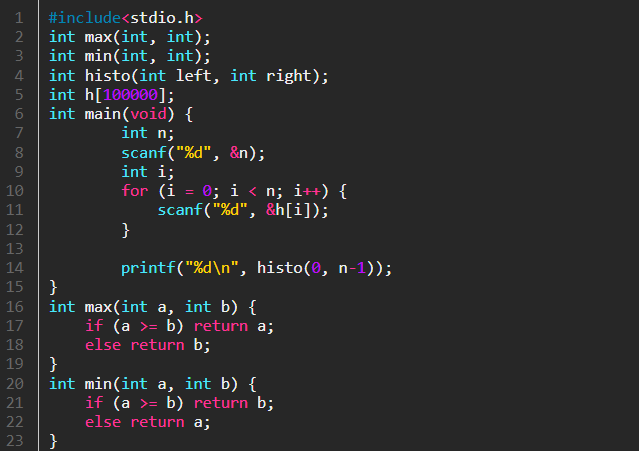
우선 main 함수는 위와 같다.
C++이 아닌 C언어로 작성하였기 때문에 max와 min 함수를 따로 정의해주었다.
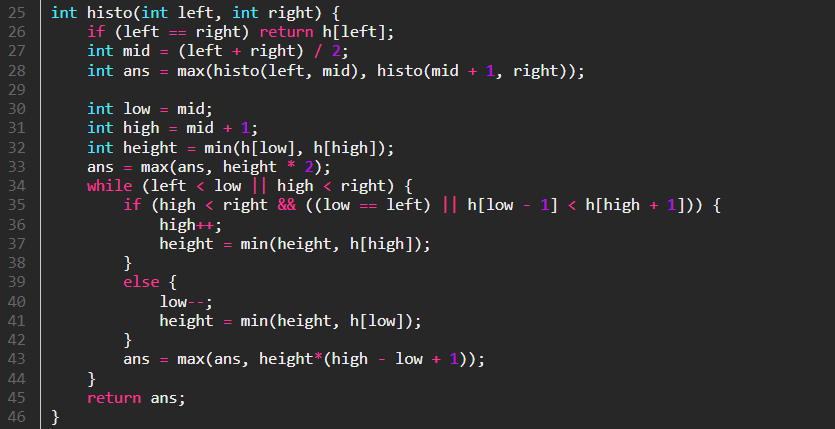
최대 직사각형을 구하는 재귀함수 histo를 정의하였다.
26) 우선 left와 right가 같은 경우는 하나의 막대인 경우이고, 이 막대의 너비는 1이므로 높이와 넓이가 같다.
따라서 넓이를 높이로 바로 return 해준다.
27, 28) 그리고 막대그래프의 중간 부분을 설정하여 왼쪽 부분과 오른쪽 부분을 각각 재귀호출해준다.
막대가 1개일 때 최대 직사각형인 경우가 아니라면 결국 반드시 최대 직사각형이
왼쪽 부분과 오른쪽 부분이 겹치는 경우로 나오게 된다.
30~32) 중간을 기준으로 양쪽의 막대중에 높이가 작은 막대를 height로 설정해준다.
33) 제일 처음 단계에는 막대 하나의 값 (h[left]) 과 height*2 를 비교하게 될 것이다.
즉, 재귀호출의 가장 아래단계를 의미한다.
이후부터는 43번째 줄 코드에서 최대 직사각형인지 비교한다.
34~44) 중간을 기준으로 왼쪽 부분문제와 오른쪽 부분문제로 확장해나가는 과정이다.

PC로 보시는 것을 권장합니다.
피드백은 항상 환영입니다.
'알고리즘 > 백준 문제풀이' 카테고리의 다른 글
| [BOJ 2568] 전깃줄 - 2 (0) | 2020.04.22 |
|---|---|
| [BOJ 11066] 파일 합치기 (0) | 2019.07.22 |
| [BOJ 1992] 쿼드트리 (0) | 2019.03.30 |
| [BOJ 2166] 다각형의 면적 (0) | 2019.02.27 |
| [BOJ 2399] 거리의 차이 (0) | 2019.01.28 |