본문 바로가기
알고리즘

LIS (Longest Increasing Subsequence) - 최장 증가 부분 수열

Rebro 2020. 4. 22. 13:11
728x90
반응형

주어진 수열에서 <최장 증가 부분 수열 (Longest Increasing Subsequence)> 을 구하는 문제 유형을 알아보자. 

 

사실 이 유형은 DP(Dynamic Programming) 문제로 자주 나오는 유형이며, O(N^2)의 시간복잡도를 갖는 알고리즘과 O(NlogN)의 시간 복잡도를 갖는 알고리즘이 있다. 

(당연히 어려운 문제로는 NlogN을 요구하는 문제가 나온다...)

[개념]

 

LIS의 개념은 단어 그대로 가장 긴 증가하는 부분 수열을 구하는 것이다. 

어떠한 수열이 주어질 때, 그 수열에서 일부 원소를 뽑아내어 새로 만든 수열을 '부분 수열'이라고 하며, 이 수열이 오름차순을 유지하면 '증가하는 부분 수열'이 되는 것이다. 

그러므로 어떤 수열에서 만들 수 있는 부분 수열 중에서 가장 길면서 오름차순을 유지하는 수열이 LIS이다.

 

예를 들어 위와 같은 길이가 8인 수열이 주어진다고 하자.

이 수열에서 증가하는 부분 수열을 뽑는다면 다음과 같이 여러 수열이 나올 것이다. 

[2, 3] , [1, 3] , [2,5] , [2,3,5] , [1,3,5] ....

 

그 중에서 가장 길이가 긴 수열은 [2,3,5,6,7] 이다. 

물론 [1,3,5,6,7] 도 가장 길이가 긴 수열로 가능하며, 이와 같이 LIS는 반드시 하나로 결정되는 것은 아니다.

따라서 문제에서도 답으로 LIS의 길이를 출력하도록 하거나, 수열을 구한다면 답이 여러 개가 되도록 출제된다.

 

 

[알고리즘]

 

1. O(n^2)의 시간복잡도

 

O(n^2)의 시간복잡도를 갖는 알고리즘은 꽤나 간단하다. 

 

문제 출처 : https://www.acmicpc.net/problem/11053

 

11053번: 가장 긴 증가하는 부분 수열

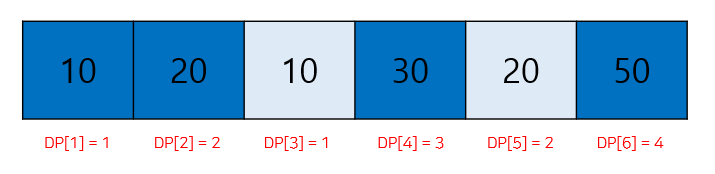
수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구하는 프로그램을 작성하시오. 예를 들어, 수열 A = {10, 20, 10, 30, 20, 50} 인 경우에 가장 긴 증가하는 부분 수열은 A = {10, 20, 10, 30, 20, 50} 이고, 길이는 4이다.

www.acmicpc.net

1) 수열의 길이와 같은 dp배열을 하나 선언한다. 

 

2) 수열을 처음부터 끝까지 순서대로 1개씩 탐색한다. ( 현재 위치 = i )

 

  (1) dp[i]에 넣을 값을 초기화해준다. (val)

  (2) 현재 위치(i)보다 이전에 있는 원소(j) 중에서 현재 원소보다 작은지 체크한다. (크거나 같으면 LIS 불가능)

  (3) 현재 원소보다 작다면, dp[j]가 val 보다 큰지 체크한다. 이 때 val보다 크다면 j번째 원소를 포함했을 때가,

       지금까지 확인한 최장 증가 부분 수열보다 더 길다는 의미이므로 val에 dp[j]를 할당해준다. 

  (4) 현재 원소도 포함해주어야 하므로 최종적으로 dp[i]에 val + 1을 할당해준다.

 

3) dp배열의 원소 중에서 가장 큰 값을 출력한다. 

 

예) [10, 20, 10, 30, 20, 50]

소스 코드는 아래와 같다. 

 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
//BOJ 11053 가장 긴 증가하는 부분 수열
#include<iostream>
 
using namespace std;
int arr[1001]; 
int dp[1001];
 
int main(void) {
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> arr[i];
    dp[1] = 1;
    for (int i = 2; i <= n; i++) {
        int val = 0;
        for (int j = 1; j < i; j++) {
            if (arr[j] < arr[i]) {
                if (val < dp[j]) val = dp[j];
            }
        }
        dp[i] = val + 1;
    }
    int ans = 0;
    for (int i = 1; i <= n; i++) {
        if (ans < dp[i]) ans = dp[i];
    }
    cout << ans;
}

 

 

2. O(nlogn)의 시간복잡도 - 길이만 구하기

 

위의 알고리즘은 배열의 원소를 하나씩 탐색하면서, 그 이전의 원소들을 모두 탐색하기 때문에 O(n^2)의 시간복잡도를 갖는다. 따라서 n이 10000보다 커지게 되면 시간이 매우 오래 걸리게 된다.

 

이에 대한 해결법으로 O(nlogn)의 시간복잡도를 갖는 알고리즘을 이용해야 하는데, 이 알고리즘을 위해서는 lower_bound를 이용해야 한다. 

 

즉, 원래의 O(n^2) 알고리즘에서 이전의 원소들을 탐색하는 과정(O(n)) 을 lower_bound(O(logn))을 이용하여 시간을 줄여주는 것이다. 

 

핵심 아이디어는, LIS를 만들기 위해서는 만드는 과정에서 LIS의 마지막 원소가 가능한 작을수록 더 긴 LIS를 생성할 수 있다는 것이다.

그러므로 원소가 들어올 때, 만약 현재 생성된 LIS의 마지막 원소보다 작은 경우, LIS에 들어갈 위치를 찾은 후(O(logn)) 원소를 대체한다. 

 

간단한 예시로, [1, 2, 3, 7, 5, 6] 수열이 있을 때, 5까지 탐색을 한 경우 가능한 LIS는

[1, 2, 3, 7], [1, 2, 3, 5] 두가지가 만들어 진다. 

이 때, 우리가 구하고자 하는 것은 최장 길이를 가지기만 하면 되므로 둘 다 LIS를 만족하는데, 더 긴 LIS를 만들기 위해서는 [1, 2, 3, 7] 보단 [1, 2, 3, 5]가 적합하다.

실제로 마지막 원소 6이 들어올 때에는 [1, 2, 3, 7]로는 생성할 수 없고, [1, 2, 3, 5]에 붙어 [1, 2, 3, 5, 6]을 만들 수 있다.

 

이러한 원리로 차례대로 원소가 들어올 때, 다음과 같은 과정을 거친다. 

 

1. [1]

2. [1, 2]  (2>1)

3. [1, 2, 3]  (3>2)

4. [1, 2, 3, 7]  (7>3)

5. [1, 2, 3, 5]  (5 < 7. 5가 들어갈 자리를 찾은 후 7이 5로 대체 됨)

6. [1, 2, 3, 5, 6] (6 > 5)

 

이처럼 LIS의 길이를 구하기 위해서는 LIS를 만족하는 수열을 담기 위한 배열을 따로 선언해야 한다.

이 배열을 K라고 하자. 

원소를 처음부터 하나씩 보면서, 이전까지 범위에서의 LIS의 마지막 원소보다 더 크면 바로 뒤에 붙여준다.

 

[10, 20, 10, 30, 20, 50] 배열을 예로 들면

 

1. K = [10]

2. K = [10, 20]

3. K = [10, 20]  (10이 첫번째 자리로 들어감)

4. K = [10, 20, 30]

5. K = [10, 20, 30] (20이 두번째 자리로 들어감)

6. K = [10, 20, 30, 50]  

따라서 LIS는 [10, 20, 30, 50] 이 만들어지고 길이는 4로 나오게 된다. 

 

[10, 20, 10, 30, 25, 50] 배열을 예로 들면

 

1. K = [10]

2. K = [10, 20]

3. K = [10, 20] (10이 첫번째 자리로 들어감)

4. K = [10, 20, 30]

5. K = [10, 20, 25] (25가 세번째 자리로 들어감)

6. K = [10, 20, 25, 50] 으로 나오게 된다. 

 

이처럼 위의 알고리즘을 이용하면 K배열에 항상 LIS가 만들어지는 것 같지만 실제로는 이 알고리즘을 이용하면 길이만 구할 수 있게 된다. 

 

[3, 5, 2, 6, 1] 배열은 다음과 같이 진행이 된다. 

1. K = [3]

2. K = [3, 5]

3. K = [2, 5]

4. K = [2, 5, 6]

5. K = [1, 5, 6]

 

실제로 LIS는 [3, 5, 6]이지만 K에는 [3, 5, 2, 6, 1]로는 만들어 질 수 없는 부분수열인 [1, 5, 6]이 들어가게 된다.

단순히 길이를 구하는 목적이라면 이는 답에 영향을 주지는 않는다. 

 

1까지 탐색했을 때, LIS의 길이가 3인데,

만약 6보다 큰 수가 들어온다면 [1, 5, 6] 뒤에 붙게 되는데 이는 결국 [3, 5, 6] 뒤에 붙는 것이랑 길이 측면에서는 차이가 없게 된다. 

만약 6보다 작은 수가 들어온다면 어차피 [3, 5, 6] 에는 붙을 수 없고, [1, 5, 6]에서도 단순히 교체만 되기 때문에 길이는 3으로 그대로 유지가 된다. 

 

이러한 원리로 LIS의 길이는 구할 수 있지만, 실제 LIS를 이루는 부분 수열을 구하기 위해서는 추가적인 작업이 필요하다. 

 

문제 출처 : https://www.acmicpc.net/problem/12015

 

12015번: 가장 긴 증가하는 부분 수열 2

첫째 줄에 수열 A의 크기 N (1 ≤ N ≤ 1,000,000)이 주어진다. 둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (1 ≤ Ai ≤ 1,000,000)

www.acmicpc.net

소스코드는 아래와 같다.

 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
//BOJ 12015 가장 긴 증가하는 부분 수열 2
#include<iostream>
#include<algorithm>
 
using namespace std;
int arr[1000001];
int L[1000001];
int main(void) {
    ios::sync_with_stdio(false);
    cin.tie(NULL);
 
    int n; cin >> n;
    int temp;
    int idx = 0;
    for (int i = 1; i <= n; i++) {
        cin >> temp;
        if (idx == 0) L[idx++] = temp;
        else {
            if (L[idx - 1] < temp) L[idx++] = temp;
            else {
                L[lower_bound(L, L + idx, temp) - L] = temp;
            }
        }
    }
    cout << idx;
}
 

 

3. O(nlogn)의 시간복잡도 - 길이와 수열 모두 구하기

2번의 알고리즘을 통해서 nlogn의 시간복잡도로 LIS의 길이까지 구하였다. 

그렇다면 LIS를 이루는 부분수열도 구하기 위해서는 어떤 작업을 거쳐야 할까?

 

2번의 알고리즘에서 주어진 수열의 각각의 원소들이 K 배열에 들어가는 index를 배열로 별도로 저장한다. 

그리고 나서 마지막원소부터 LIS의 길이를 감소시켜 가면서, 처음으로 해당 길이의 index가 나오는 원소만 뽑아낸다. 

 

[3, 5, 2, 6, 1] 배열을 예로 들면, 

1. K = [3]

2. K = [3, 5]

3. K = [2, 5]

4. K = [2, 5, 6]

5. K = [1, 5, 6]

 

이므로 3은 1번째, 5는 2번째, 2는 1번째, 6은 3번째, 1은 1번째 index에 들어가게 된다. 

즉, index 배열은 [1, 2, 1, 3, 1]이 되는 것이다. 

LIS의 길이는 현재 3이므로 index 배열의 뒤에서부터 처음으로 3이 나오는 원소는 6이며, 

그 다음 처음으로 2가 나오는 원소는 5, 그 다음 처음으로 1이 나오는 원소는 3이 된다. 

따라서 이를 역으로 정렬하면 [3, 5, 6] 으로 우리가 구하고자 하는 LIS가 나오게 된다. 

 

소스코드를 통해서 이해한다면 더 이해하기가 쉬울 것 같다. 

 

문제 출처 : https://www.acmicpc.net/problem/14003

 

14003번: 가장 긴 증가하는 부분 수열 5

첫째 줄에 수열 A의 크기 N (1 ≤ N ≤ 1,000,000)이 주어진다. 둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (-1,000,000,000 ≤ Ai ≤ 1,000,000,000)

www.acmicpc.net

소스 코드)

 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include<iostream>
#include<algorithm>
 
using namespace std;
int arr[1000001];
int L[1000001];
int index[1000001];
int ans[1000001];
int main(void) {
    ios::sync_with_stdio(false);
    cin.tie(NULL);
 
    int n; cin >> n;
    int temp;
    int idx = 0;
    for (int i = 1; i <= n; i++) {
        cin >> temp;
        arr[i] = temp;
        if (idx == 0) {
            L[idx++] = temp;
            index[i] = 0; // first location = 0
        }
        else {
            if (L[idx - 1] < temp)
            {
                index[i] = idx;
                L[idx++] = temp;
            }
            else {
                index[i] = lower_bound(L, L + idx, temp) - L;
                L[lower_bound(L, L + idx, temp) - L] = temp;
            }
        }
    }
    int t = 0;
    cout << idx << '\n';
    for (int i = n; i >= 1; i--) {
        if (idx == index[i]+1) {
            ans[t++] = arr[i];
            idx--;
        }
    }
    for (int i = t-1; i >=0; i--) cout << ans[i] << ' ';
}
 
728x90
반응형
저작자표시동일조건

'알고리즘' 카테고리의 다른 글

최소 / 최대 맨해튼 거리 (Manhattan Distance)  (0) 2020.09.17
완전 탐색 (Brute-Force Search / Exhaustive Search) 알고리즘  (0) 2020.09.11
LIS (Longest Increasing Subsequence) - 최장 증가 부분 수열  (3) 2020.04.22
Knuth's Optimization  (0) 2019.07.22
볼록 껍질 (Convex Hull)  (4) 2019.03.10
CCW (Counter-ClockWise) - (2)  (0) 2019.02.27

태그

, , , , ,

'알고리즘' Related Articles

티스토리툴바