1. 트로미노란?
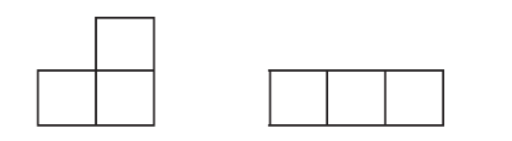
트로미노(Tromino)란, n=3인 폴리오미노(polyomino)로, 크기가 같은 정사각형 3개를 변끼리 붙여 만든 다각형이다. 따라서 다음과 같이 두 개의 트로미노가 존재할 수 있다.
2. $2^n$ x $2^n$ L-트로미노 타일링
이제, 이 트로미노중에서 일자형이 아닌 L 모양의 트로미노를 한 변의 길이가 $2^n$인 정사각형에 배치하는 것이 목표이다.
결론부터 말하자면, L-트로미노는 1x1 한 칸을 제외하고, 한 변의 길이가 $2^n$인 정사각형을 항상 채울 수 있다.
증명은 다음과 같이 수학적 귀납법으로 가능하다.
[정리] $2^n$ X $2^n$ 크기의 정사각형에 1x1 한 칸을 제외하고 항상 L-트로미노로 모두 채울 수 있다.
[증명]
1. n = 1일 때
n = 1인 경우는 자명하다. 2x2 크기의 정사각형에 L-트로미노 하나를 넣으면 1x1 한 칸을 제외하고 채울 수 있다.

2. n = k일 때 참이라고 가정
n = k일 때, 즉 정사각형의 한 변이 $2^k$일 때, L-트로미노로 한 칸을 제외하고 모두 채울 수 있다고 가정하자.

3. n = k+1일 때
n = k일 때 참이라고 가정한다면, 다음 그림과 같이 n = k+1일 때에도 한 칸을 제외하고 L-트로미노로 한 변의 길이가 $2^{k+1}$인 정사각형을 채울 수 있다.

따라서, 수학적 귀납법에 의해서 위 정리는 모든 자연수 n에 대해서 항상 참이다.
3. 소스 코드 / 예제 문제
14601번: 샤워실 바닥 깔기 (Large)
첫 번째 줄에는 바닥의 한 변의 길이를 표현하는 자연수 K(1 ≤ K ≤ 7) 가 주어진다. 이때 바닥의 크기는 2K 가 됨에 유의하라. 두 번째 줄에는 배수구의 위치를 나타내는 자연수 x, y (1 ≤ x, y ≤ 2K)
www.acmicpc.net
이 문제가 트로미노 타일링을 그대로 구현하면 되는 문제이다.
문제에서는 타일을 배치하는 방법이 존재하지 않으면 -1을 출력하라고 했지만, 실제로 배치하는 방법은 항상 존재한다.
위의 증명 과정에서 알 수 있듯이, 주어진 정사각형에 트로미노를 채우는 방법은 한 변의 크기를 절반으로 줄인 4개의 부분 정사각형을 통해서 구할 수 있다.
그러므로 '분할 정복' 기법을 이용한다.
bool check(int sz, int x, int y) {
for (int i = x; i < x + sz; i++) {
for (int j = y; j < y + sz; j++) {
if (A[i][j] != 0) return false;
}
}
return true;
}
void sol(int sz, int x, int y) {
num++;
int s = sz / 2;
if (check(s, x, y)) A[x + s - 1][y + s - 1] = num;
if (check(s, x, y + s)) A[x + s - 1][y + s] = num;
if (check(s, x + s, y)) A[x + s][y + s - 1] = num;
if (check(s, x + s, y + s)) A[x + s][y + s] = num;
if (sz == 2) return;
sol(s, x, y);
sol(s, x + s, y);
sol(s, x, y + s);
sol(s, x + s, y + s);
}
check 함수는 현재 주어진 정사각형이 모두 비어있는지를 체크하는 함수이다.
모두 비어있다면, sol 함수에서 해당 정사각형에는 한 칸을 제외하고 L-트로미노를 채울 수 있기 때문에 제외되는 한 칸(꼭짓점)에 num으로 숫자를 부여해준다.
즉, 위 증명과정에서 n=k+1인 경우의 그림을 통해 이해해보면, 노란색 부분을 채워주는 과정이다.
오른쪽 위 꼭짓점이 배수구라고 가정하면 1 사분면의 사각형은 check함수에서 false를 반환한다.
나머지는 true를 반환하므로 노란색 부분에 num이 채워지게 되는 것이다.
이후에 재귀 함수를 통해서 분할 정복을 이용하면 된다.
PC로 보시는 것을 권장합니다.
피드백은 언제나 환영입니다. 댓글로 달아주세요 ^-^
'알고리즘' 카테고리의 다른 글
| [자료구조] 트라이(Trie) 자료구조 (3) | 2020.12.13 |
|---|---|
| [DFS] 그래프 간선의 분류 / 사이클(Cycle) 찾기 (0) | 2020.11.10 |
| 비트마스크 (BitMask) 알고리즘 (3) | 2020.10.15 |
| 최소 / 최대 맨해튼 거리 (Manhattan Distance) (0) | 2020.09.17 |
| 완전 탐색 (Brute-Force Search / Exhaustive Search) 알고리즘 (0) | 2020.09.11 |



