[문제]
5821번: 쌀 창고
첫째 줄에 R, L, B가 주어진다. 둘째 줄부터 R개 줄에는 X[i]가 주어진다. (1 ≤ R ≤ 100,000, 1 ≤ L ≤ 1,000,000,000, 0 ≤ B ≤ 2,000,000,000,000,000)
www.acmicpc.net
[난이도]
- Platinum 4 (solved.ac 20.10.29 기준)
[필요 개념]
- 이분 탐색 (Binary Search)
- 누적 합 (Prefix Sum)
[풀이]
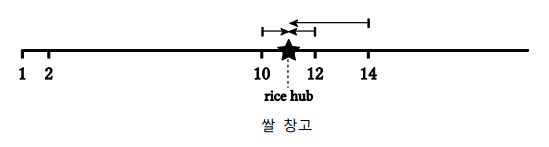
각 논들이 일직선상에 주어져 있고, 해당 논을 수확하기 위해서는 쌀 창고와의 거리만큼 비용이 필요하다.
지불할 수 있는 비용 한도가 정해져 있고, 한도 내에서 쌀 창고의 위치를 잘 정해줘서 수확할 수 있는 최대의 논 수를 구하는 것이 목적이다.
우선, 비용 한도를 신경쓰지 않고, 주어진 논들을 모두 수확할 때 비용이 최소가 되기 위해서는 가운데 위치한 논 위에 쌀 창고가 있어야 한다.
예를 들어서 현재 쌀 창고 기준으로 왼쪽에 논이 a개, 오른쪽에 b개가 있다고 가정하자.
현재 쌀 창고를 오른쪽으로 1만큼 이동시키면 왼쪽의 논과의 거리는 1씩 멀어지고, 오른쪽 논과의 거리는 1씩 가까워진다.
즉, 비용이 a-b만큼 더해진다.
반대로 왼쪽으로 1만큼 이동시키면 b-a만큼 더해진다.
따라서 비용이 최소인 경우는 결국, 좌우로 이동시켜도 비용이 감소하지 않는 경우이기 때문에 a = b인 경우이다.
즉, n개의 논이 있다면 n/2번째 논의 위치에 쌀 창고가 있어야 한다.
(n이 짝수인 경우에는 n/2번째 또는 n/2 + 1 번째 둘 다 가능하다. 직접 예시를 만들어보면 쉽게 이해가 가능하다.)
위의 내용을 이용하면 수확 가능한 논이 정해지면 필요한 비용도 자동으로 정해진다는 의미이다.
따라서 구간을 정하면 비용은 전처리해둔 prefix sum을 이용하면 O(1)만에 계산이 가능하다.
그 후, 비용 한도 B 이하를 가지면서 가장 긴 구간을 구하기만 하면 되는데,
구간의 시작점을 고정시켜놓고 비용한도를 초과하지 않는 구간의 끝 점 중 가장 오른쪽에 있는 점을 이분 탐색으로 구한다.
따라서 O(RlogR)의 시간 복잡도를 갖는다.
[소스 코드]
#include<bits/stdc++.h>
#define FOR(i, j, k) for(int i = j; i<=k; i++)
using namespace std;
using ll = long long;
ll X[100001];
ll psum[100001];
int main(void) {
ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
ll R, L, B; cin >> R >> L >> B;
FOR(i, 1, R) {
cin >> X[i];
psum[i] = psum[i - 1] + X[i];
}
int ans = 0;
FOR(i, 1, R) {
int s = i;
int e = R;
while (s <= e) {
int mid = (s + e) / 2;
int k = (i + mid) / 2;
ll tmp = 0;
tmp += psum[mid] - psum[k] - (X[k] * (mid - k)); //right
tmp += X[k] * (k - i) - (psum[k - 1] - psum[i - 1]); //left
if (tmp <= B) {
ans = max(ans, mid - i + 1);
s = mid + 1;
}
else e = mid - 1;
}
}
cout << ans;
}
PC로 보시는 것을 권장합니다.
피드백은 언제나 환영입니다. 댓글로 달아주세요 ^-^
'알고리즘 > 백준 문제풀이' 카테고리의 다른 글
| [BOJ 1533] 길의 개수 (0) | 2020.11.28 |
|---|---|
| [BOJ 1073] 도미노 (0) | 2020.11.06 |
| [BOJ 2672] 여러 직사각형의 전체 면적 구하기 (2) | 2020.10.28 |
| [BOJ 2336] 굉장한 학생 (0) | 2020.08.05 |
| [BOJ 2437] 저울 (0) | 2020.07.10 |
