주어진 문제의 답이 단조성을 갖는 경우에는 Parametric Search를 이용하여 해당 문제를 해결할 수 있다.
Parametric Search에 대해서 이미 잘 알고 있다면 스크롤을 아래로 내리자.
예를 들어 "N명의 사람이 나이순으로 정렬되어 있을 때, 20세 이상이면서 나이가 가장 작은 사람의 나이를 구하시오"와 같은 문제가 있다고 하자.
앞에서부터 다 확인한다면 O(N)의 시간이 걸리게 되지만, Parametric Search를 이용하면 O(logN)만에 해결할 수 있다.
먼저, 답이 될 수 있는 범위의 중간지점을 확인한다.
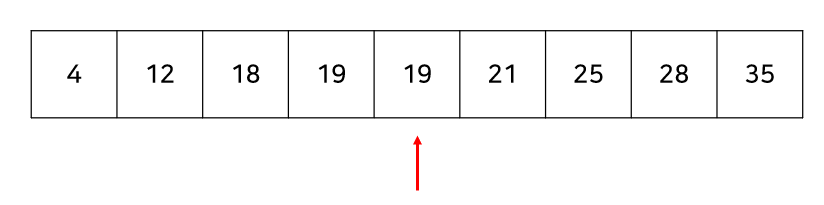
19는 20세 미만이므로 답이 될 수 없다. 그러면 현재 위치보다 왼쪽에 있는 나이들은 당연히 19 이하이기 때문에 답이 될 수 없다. 따라서 왼쪽은 더 이상 볼 필요가 없다.

그다음 또 가능한 범위에서 중간지점을 확인해보자. 25는 20세 이상이므로 답이 될 수도 있다. 하지만 25보다 왼쪽에 있으면서 살아있는 값이 존재하기 때문에, 이 값들도 답이 될 가능성이 있으므로 확인해주어야 한다.
25보다 오른쪽에 있는 값들은 답이 될 수 없다. 이미 25보다 크기 때문에 최소인 나이에 해당하지 않게 된다.

이런 과정을 반복하면 21이라는 답을 구해낼 수 있다.
이처럼 Parametric Search란, 최적화하는 문제를 '결정 문제'로 바꿔서 해결하는 방법을 말한다.
20세 이상이면서 최소 나이를 구하는 상황을 각 나이별로 "20세 이하인가?"의 문제에 대한 참, 거짓을 반환하게 만들어서 해결하는 방식이다.
여기서 답이 단조성을 갖는다는 말은, 20세 이상인 사람들이 중간에 끊어지는 형태가 아니라 이어지게 나타나는 것을 말한다. 만약 그렇지 않다면 위처럼 답이 되지 않는 왼쪽이나 오른쪽 부분을 모두 제외할 수 없기 때문이다.
종종 Parametric Search와 이분 탐색(Binary Search)을 헷갈리는 경우가 있는데, 과정 자체는 동일하나 개념적으로는 약간의 차이가 있다.
이분 탐색은 "원하는 값이 존재하는지, 존재한다면 어디 있는지?"를 찾는 과정이고, Parametric Search는 "조건을 만족하는 값 중 최소/최대가 어디 있는가?"를 찾는 과정이라고 생각하면 될 것 같다.
사실 문제풀이를 진행할 때에는 딱히 이런 자세한 부분까지 신경 쓰진 않는다.
앞에서 기본적인 Parametric Search에 대해서 알아보았다. 아마 이 게시글을 들어온 사람이라면 위의 내용은 이미 잘 숙지하고 있을 것이라고 생각한다.
그러면 병렬 이분 탐색(Parallel Binary Search, PBS)이란 뭘까?
쉽게 말하면 '여러 결정 문제에 대해서 동시에 Parametric Search를 진행하는 것'이다.
병렬 이분 탐색은 실제로 정해가 아니지만 병렬 이분 탐색으로 풀리는 문제가 꽤 있으므로 알아두면 유용하게 써먹을 수 있다.
사실 병렬 이분 탐색은 알고리즘보단 기법에 가까운 느낌이기 때문에 바로 문제를 통해서 설명하겠다.
https://www.acmicpc.net/problem/1396
1396번: 크루스칼의 공
첫째 줄에는 그래프의 정점의 개수 n과 간선의 개수 m이 주어진다. 그리고 두 번째 줄에서 m+1번째 줄까지는 a b c의 형태로 a와 b를 잇는 간선의 고유값이 c라는 의미이다. m+2번째 줄에는 알고 싶은
www.acmicpc.net
병렬 이분 탐색의 가장 대표적인 문제이다.
먼저, 이 문제에서 쿼리의 개수가 1개라고 가정해보자.
크루스칼 알고리즘을 이용하여 고유값이 작은 간선부터 정점들을 하나씩 연결해가다가 x와 y가 같은 컴포넌트에 속하는 순간의 간선의 고유값이 x→y로 이동하기 위한 최소 온도가 된다.
그리고 이때 x와 같은 컴포넌트에 속하는 정점의 개수가 이동 가능한 범위 안의 정점 개수이다.
따라서, 쿼리가 1개인 경우에는 시간 복잡도가 O(mlogm + mlog*n) = O(mlogm)이 된다.
간선을 정렬하는데 O(mlogm), 크루스칼 알고리즘을 적용하는데 O(mlog*n)의 시간이 필요하게 된다.
만약 쿼리의 개수가 Q개 들어온다면 간선은 미리 정렬해둔다고 해도, 매 쿼리마다 크루스칼 알고리즘을 수행하면 O(Qmlog*n)이 걸리게 된다.
반대로 한 번의 크루스칼 알고리즘을 통해서 간선을 하나씩 볼 때마다 모든 쿼리를 다 확인해주는 방식을 이용하더라도 O(Qmlog*n)의 시간이 필요하게 된다. 당연히 시간 내에 수행하지 못한다.
이미 우린 병렬 이분 탐색을 사용해야 한다는 것을 알고 있기 때문에, 쿼리가 1개인 경우에 이 문제를 Parametric Search를 통해서 해결해보자.
간선을 하나씩 연결해나가면서 처음으로 x와 y가 연결되는 시점을 찾는 것이 아니라, "간선을 앞에서부터 k개 연결했을 때 x와 y가 연결되어 있는가?"라는 결정문제로 바꾸어서 생각할 수 있다.
이분 탐색의 범위는 [1, m]이 될 것이고, k개 연결하는 과정은 동일하게 크루스칼 알고리즘을 이용하기 때문에 시간 복잡도는 O(logm × mlog*n)이 된다.
따라서 쿼리가 Q개 존재한다면 O(logm × Qmlog*n)으로, 오히려 처음 방법보다 시간이 더 오래 걸리게 된다.
여기서 병렬 이분 탐색은 이 시간 복잡도를 O(logm×(mlog*n + Q))로 줄여주게 된다.
핵심적인 아이디어는 각 쿼리마다 동일한 이분 탐색을 계속 수행한다는 것에서 얻을 수 있다. 따라서 이분 탐색을 수행할 때 현재의 mid, 즉 k값이 다른 쿼리에서의 k값과 일치하는 경우가 발생할 수 있다.
그런데, 이런 상황에서 각각의 쿼리마다 크루스칼 알고리즘을 수행하게 되면, k개의 간선을 연결하는 동일한 과정을 불필요하게 반복할 수밖에 없다.
그러므로, 한 번의 크루스칼 알고리즘만 수행하여 k가 동일한 쿼리들을 한 번에 처리해주는 방식을 이용하면 훨씬 효율적이다.
게다가 특정 k마다 크루스칼 알고리즘을 매번 수행할 필요 없이, 크루스칼 알고리즘을 수행하면서 현재 연결된 간선의 개수가 k인 경우에 k에 해당하는 쿼리들을 처리해주면 되므로 결국 1번의 크루스칼 알고리즘으로 모든 쿼리를 갱신할 수 있다.
따라서, 시간 복잡도가 O(mlog*n + Q)가 되고, 파라메트릭 서치를 하는 과정이 O(logm)이므로 최종적으로 O(logm×(mlog*n + Q))가 된다.
예시와 그림을 통해서 이해해보자.
[1, 10]의 구간에서 5개의 쿼리에 대해 각각 Parametric search를 수행한다고 가정한다. 아래와 같이 쿼리들이 주어져 있으며, 실제 답을 찾아가는 과정이다.
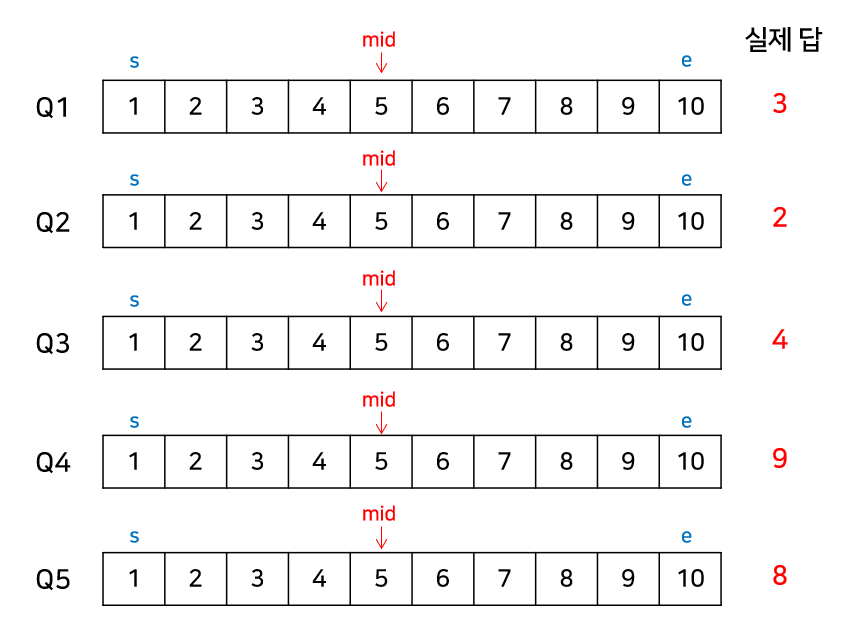
처음엔 모든 쿼리의 mid값이 5이므로 5개의 간선을 연결한 순간 모든 쿼리들을 처리해준다.
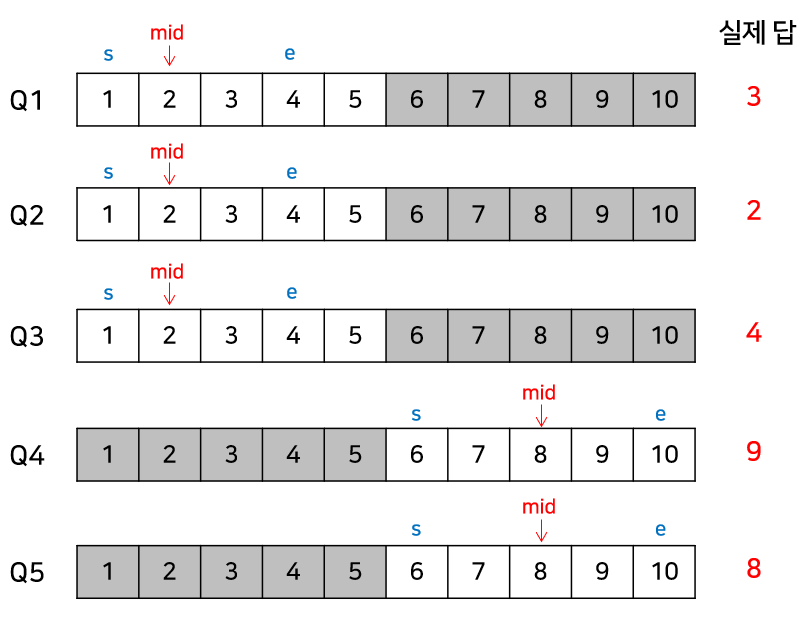
그다음엔, mid값으로 2와 8이 있다. 따라서, 간선을 2개 연결했을 때 Q1 ~ Q3을 처리하고, 간선을 8개 연결했을 때 Q4, Q5를 처리한다.
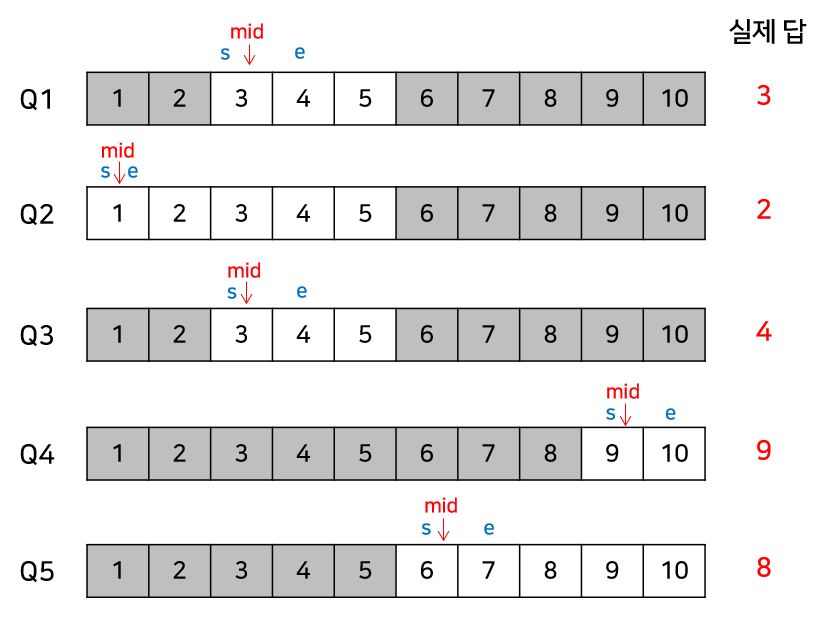


이렇게 4번의 크루스칼 알고리즘 수행으로 5개의 쿼리에 대한 답을 빠르게 구할 수 있게 된다.
코드로 구현할 땐, |e - s| 만큼의 2차원 벡터를 선언하여, 각 쿼리마다 현재 mid값인 인덱스에 쿼리의 번호를 넣어주어, 동일한 mid값에 대해서 쿼리들을 동시에 처리하게 해준다.
아래의 코드를 통해서 이해해보자.
#include<bits/stdc++.h>
#define all(v) v.begin(), v.end()
#define ini(x, y) memset(x, y, sizeof(x));
#define pb push_back
#define fi first
#define se second
using namespace std;
using pii = pair<int, int>;
int P[101010], l[101010], r[101010];
pii ans[101010];
vector<int> g[101010];
int find(int a) {
return P[a] < 0 ? a : P[a] = find(P[a]);
}
void merge(int a, int b) {
a = find(a);
b = find(b);
if (a != b) {
if (P[a] > P[b]) swap(a, b);
P[a] += P[b];
P[b] = a;
}
}
int main(void) {
ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
int n, m; cin >> n >> m;
vector<tuple<int, int, int>> edge;
for (int i = 0; i < m; i++) {
int a, b, c; cin >> a >> b >> c;
edge.pb(make_tuple(c, a, b));
}
sort(all(edge));
int q; cin >> q;
vector<pii> query(q);
for (int i = 0; i < q; i++) {
cin >> query[i].fi >> query[i].se;
}
for (int i = 0; i < q; i++) l[i] = 1, r[i] = m;
while (1) {
for (int i = 1; i <= m; i++) g[i].clear();
bool chk = false;
for (int i = 0; i < q; i++) {
if (l[i] <= r[i]) {
chk = true;
g[(l[i] + r[i]) / 2].pb(i);
}
}
if (!chk) break;
ini(P, -1);
int i = 1;
for (auto [c, a, b] : edge) {
merge(a, b);
for (int j : g[i]) {
if (find(query[j].fi) == find(query[j].se)) {
ans[j].fi = c;
ans[j].se = abs(P[find(query[j].fi)]);
r[j] = i - 1;
}
else l[j] = i + 1;
}
i++;
}
}
for (int i = 0; i < q; i++) {
if (l[i] > m) cout << -1 << '\n';
else cout << ans[i].fi << ' ' << ans[i].se << '\n';
}
}
g가 각 mid값 별로 쿼리 번호들을 저장하는 이차원 벡터이다. 그리고 l, r배열은 쿼리 번호를 인덱스로 가지며, 각 쿼리의 탐색 범위를 저장해둔다.
더 이상 처리되지 않은 쿼리가 없는 경우 if(!chk) break를 통해서 while문을 종료시켜준다.
[추천 문제]
[BOJ 1396] 크루스칼의 공 (Platinum I)
[BOJ 8217] 유성 (Diamond IV)
[BOJ 5542] JOI 국가의 행사 (Diamond V)
[BOJ 15957] 음악 추천 (Diamond IV)
[BOJ 16977] 히스토그램에서 가장 큰 직사각형과 쿼리 (Diamond III)
PC로 보시는 것을 권장합니다.
피드백은 언제나 환영입니다. 댓글로 달아주세요 ^-^
'알고리즘' 카테고리의 다른 글
| [알고리즘] Lazy Propagation (Segment / Fenwick Tree) (6) | 2020.12.24 |
|---|---|
| [자료구조] 트라이(Trie) 자료구조 (3) | 2020.12.13 |
| [DFS] 그래프 간선의 분류 / 사이클(Cycle) 찾기 (0) | 2020.11.10 |
| [분할 정복] L-트로미노(L-Tromino) 타일링 (0) | 2020.10.16 |
| 비트마스크 (BitMask) 알고리즘 (3) | 2020.10.15 |



